NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 27/05/2019 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Nombres
Débutants Géométrie	NOMBRE D'OR				Glossaire NOMBRE D'OR
INDEX Suite de Fibonacci Trigonométrie	Tour d'horizon	Valeurs	Phi et Fibonacci	Proportion
	Introduction	Formules	Puissances	Construction
	Historique	Fraction continue	Trigonométrie	Géométrie
		Sommaire de cette page >>> Angles liés au nombre d'or PHI >>> PHI et lignes trigonométriques >>> Équation trigonométrique en OR

PHI ET TRIGONOMÉTRIE

= 2 cos 36° = 2 x 0,809 … = 1, 618…

1 / = 2 sin 18° = 2 x 0,309 … = 0, 618 …

36° Angle d'une branche d'une étoile à cinq branches;

C'est le tiers de l'angle au sommet d'un pentagone.

137,5° = 306 / Angle d'or, célèbre en phyllotaxie

Angles liés au nombre d'or: 36°

Quel est l'angle dont le sinus est égal au nombre d'or? Même chose pour les autres lignes trigonométriques.

Degrés	18°	36°	54°	72°
Nom	/ 10	/ 5	3 / 10	2 / 5
Radians	0,314	0,628	0,942	1,257
Sinus	0,309	0,588	0,809	0,951
Cosinus	0,951	0,809	0,588	0,309
Tangente	0,325	0,727	1,376	3,078

1,618 … = Φ; 0,809… = Φ/2 et 0,309 … = 1/(2Φ).

Suite en Trigonométrie du pentagone

Les valeurs en rouge sont des formes cachées du nombre d'or; desquelles on déduit les relations suivantes:

sin 18° = 1/(2Φ)	sin 54° = Φ/2
cos 72° = 1/(2Φ)	cos 36° = Φ/2

En fait, que deux valeurs, car le sinus de l'un est égal au cosinus du complémentaire (18°+ 72° = 90° et 36° + 54° = 90°).

Φ = 2 sin 3/10 = 2 cos /5

1/Φ = 2 sin /10 = 2 cos 2/5

Ces deux valeurs sont la base de construction des triangles d'or, dont celui à 36° représente l'angle des étoiles à cinq branches.

Valeurs trigonométriques

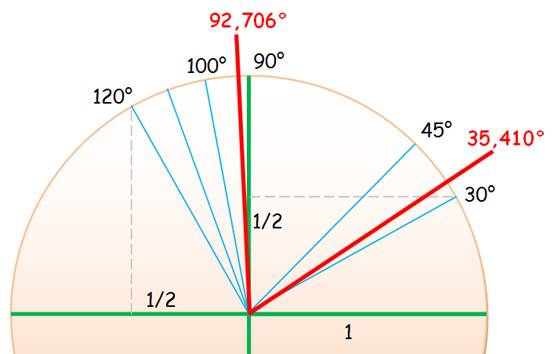
Si le nombre d'or était un angle

Il serait à peine plus grand qu'un angle droit.

Nom	Radians	Degrés décimaux	Degrés sexagésimaux
30°	0,52359878	30° =	30°
1/PHI	0,61803399	35,4107392° =	35°	24'	38"	,6610027
45°	0,78539816	45° =	45°
1 radian	1	57,2957795° =	57°	17'	44"	,8062471
Angle droit	1,57079633	90° =	90°
PHI	1,61803399	92,7065186° =	92°	42'	23"	,46703604
2 radians	2	114,591559° =	114°	35'	29"	,61249419

Illustration

Nom	Sinus	Cosinus	Tangente	Cotangente
Φ	0,99888	– 0,04722	– 21,15380	– 0,04727
1/Φ	0,57943	0,81501	0,71094	1,40657

Curiosité: arcsin(1/Φ) = 0,666 2394328 …

Équation trigonométrique en OR Curiosité – En tout cas, exercice de calcul en trigonométrie.
Évaluons sinus 2a Puis cosinus 3a	sin 2a = cos 3a =	2 sin a . cos a 4 cos^3 a – 3 cos a
Soit E la différence de ces deux expressions	E =	2 sin a . cos a – 4 cos^3 a + 3 cos a
Le cosinus est en facteur	E / cos a =	2 sin a – 4 cos^2 a + 3
Or sin² + cos² = 1	E / cos a =	2 sin a – 4 (1– sin^2 a) + 3 2 sin a – 4 + 4 sin^2 a + 3 4 sin^2 a + 2 sin a – 1
En changeant de variable: x = – 2 sin a	E / cos a =	x² – x – 1 l'équation d'or

Voir Nombre d’or et angles du pentagone régulier – Jean-Louis Breuil – 2019

Suite	Formules Pentagone et décagone et trigonométrie (table) Puissances Divine proportion
Aussi	Cercle Constante Pi Constantes Mathématiques Série du type Fibonacci et cousins Trigonométrie Trigonométrie - Exercices
DicoNombre	Nombre 0,99 888… Nombre 1,618… Nombre 35,410… Nombre 36 Nombre 57,295… Nombre 92,706…
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Geometri/NbOrTri.htm