|
|||||||||||||||||||||||||||||||||||
![]()
|
Coloration des graphes/cartes Chaine et procédé de KEMPE Très tôt, une fois le
problème posé, Kempe
trouve un procédé pour systématiser la coloration des cartes. Procédé qui
sera utilisé pour la démonstration finale. Essayons de comprendre. |
|
|
||
|
Une chaine de Kempe de couleurs
a et b (deux couleurs) est
l'ensemble des régions Il est possible de se rendre d'une région quelconque de
la chaine à une autre en restant sur ces deux couleurs. |
En termes de graphes, une chaine de Kempe de couleur a
et b est le sous-graphe connecté maximum dont les sommets sont d'une de ces
deux couleurs. Connecté veut dire que l'on peut aller d'un sommet à un
autre en passant par des arêtes existantes |
|
|
Une des techniques utilisées consiste à réduire deux
couleurs en une seule. Du fait de la définition, aucun problème de couleur
avec les régions voisines ne peut survenir. On peut toujours échanger les couleurs dans chaque
chaine. Pour résoudre le problème des quatre couleurs, on
choisit (par exemple) un couple rouge/vert et un couple bleu/jaune. |
Pour visualiser, les régions rouges/vertes sont par
exemple la Terre et les régions
bleues/vertes sont des Mers. On procède à la coloration. En cas de blocage, on
recourt à des inversions de couleurs au sein
de chaque chaine. |
|
|
Supposons que la coloration exige une cinquième
couleur: violet. |
Identifions lors de l'opération de coloration les cas
qui nécessitent cette cinquième couleur. |
|
|
Un graphe peut être momentanément
réduit (simplifier) pour poursuivre la coloration. Kempe démontre que toutes les régions réduites seront
en forme de triangles, carrés ou pentagones. |
Une fois ces réductions faites, est-ce que ces cas
inévitables subsistent? Si oui, le théorème est démontré. |
|
|
Le point crucial est de rétablir les régions réduites
sans compromettre la coloration avec quatre couleurs. |
Avec des régions triangulaires ou carrés, pas de
problème. Avec les régions pentagonales, c'est très délicat! |
|
|
|
|
|
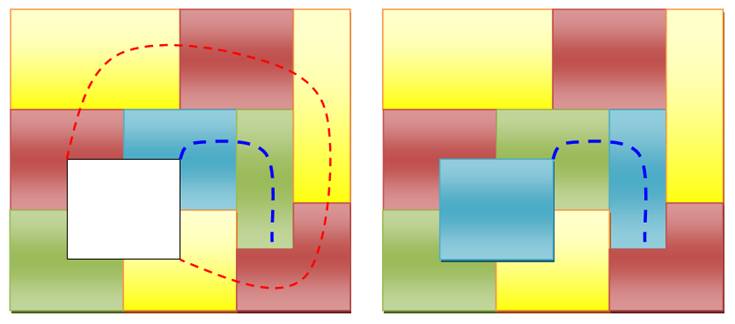
La carte est déjà colorée avec quatre couleurs. Reste
une région à colorer qui, a priori, nécessite une cinquième couleur car déjà
entourée des quatre couleurs. Nous cherchons un chaine de Kempe rouge/jaune qui réalise
un circuit partant de la zone blanche et revenant vers la zone blanche. La chaine bleu/vert qui part de la zone blanche ne peut
pas revenir vers la case blanche, car le circuit croiserait le précédent.
Par contre, rien ne nous interdit d'y inverser les
couleurs. Cela ne change pas les compatibilités avec les autres régions
rouges/jaunes. Cette inversion est bénéfique car désormais la case
blanche n'est entourée que de trois couleurs et elle peut prendre la
quatrième, ici le bleu. |
|
|
|
|
|
Cet exemple illustre d'abord une des exceptions que
n'avait pas vue Kempe. Elle est résolue cependant grâce aux inversions de
couleurs dans les chaines de Kempe. Voyez comme les choses ne sont pas
évidentes. Un ordinateur n'est pas de
trop en cas de multiplication de ce genre de cas.
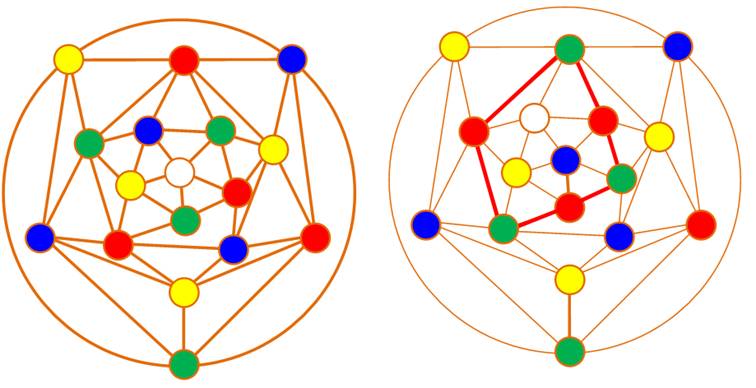
À gauche: le graphe initial proposé par Errara. La coloration est obtenue sans le sommet central
du pentagone. Celui-ci doit être réintroduit car il avait été amalgamé
momentanément pour simplifier le graphe. À droite, décision d'inverser les couleurs dans la
chaine vert/rouge indiquée. Ce qui a pour effet de pouvoir colorer le sommet
central, tout en déplaçant l'impossibilité sur un sommet voisin.
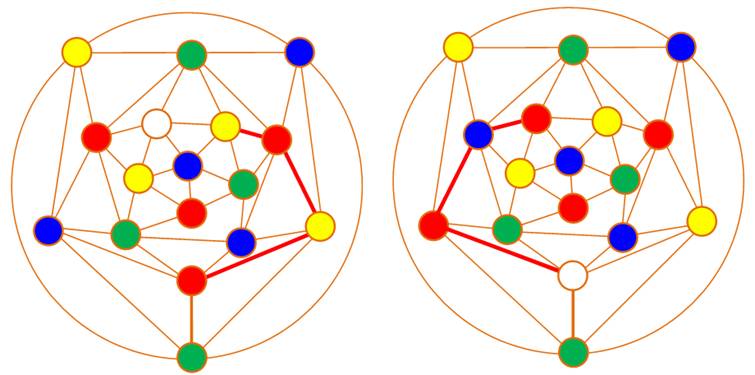
À gauche: inversion sur la chaine jaune/rouge indiquée.
Idem à droite avec pour effet de déplacer le sommet blanc.
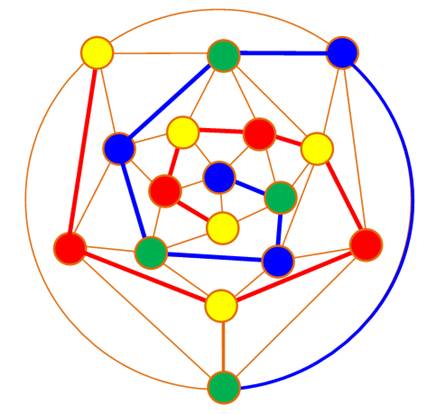
Graphe final coloré correctement. On montre les deux chaines
(la rouge et la bleue) qui forment deux spirales
enlacées. |
|
Autres exemples en Démonstration de
Kempe
D'après I. Chahit: a Victorian proof of the Four Color Theorem
![]()
|
Retour Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Topologi/aaaGraph/Kempe.htm
|
![]()