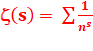|
|||||||||||||||||||||||||||||||||||||
![]()
|
HYPOTHÈSE DE RIEMANN Approches modernes Au départ, une série
qui donne la somme des inverses des nombres
élevés à une puissance En passant dans le monde des complexes (s = z), elle est devenue une fonction très prometteuse, pour expliquer la
répartition de nombres premiers. La conjecture qui lui est associée,
consiste "tout simplement" à montrer que tous les zéros de cette
fonction sont situés sur la droite des réels ayant pour valeur ½. Cette conjecture, du fait de ses nombreuses
conclusions en théorie
des nombres, est l'enjeu majeur des mathématiciens. Du même ordre que l'était le désormais
théorème de Fermat - Wiles La conjecture de Riemann est le 8e
des problèmes de Hilbert posés en 1900,
et le seul non résolu en 2010. Comme souvent en mathématiques, on a trouvé une autre conjecture équivalente (par exemple, faisant intervenir la fonction de Möbius) qui, si elle est démontrée, prouve également celle de Riemann. |
Voir ce que nous connaissons sur les zéros de la fonction zêta de Riemann
|
|
|
|
Le
calcul des racines
Démonstration
directe
|
|
|
|
|
|
Opérateur
Approche
du Français Louis de Branges
Analogie
Matrices
aléatoires infinies
|
|
|
|
|
|
Fonctions
équivalentes
Autres
Fonction
de Möbius
|
|
|
Page
réalisée à partir notamment du livre, librement interprété, de Karl Sabbagh – Dr. Riemann's zeros >>> |
|
|
|
|
Voir la publication de Philippe Biane en référence |
|
D'après Les dossiers de
La Recherche – N°50 – Août 2012
Pour
en savoir plus, voir la publication de Philippe Biane en référence
Merci à Laurent Guémappe
pour ses remarques
![]()
|
Suite |
|
|
Voir |
|
|
|
|
|
Livres |
Superbe!
Livre de poche de 500 pages qui se lit comme un roman. Raconte toute cette
recherche pour prouver la conjecture de Riemann tout en faisant quelques
détours mathématiques intéressants. Appréciable aussi, l'atmosphère du monde
des chercheurs en mathématiques.
The search for the $ 1 million solution to the
greatest problem in mathematics – Atlantic
book London – 2003 |
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Identite/RiemAppr.htm |
![]()