|
||||||||||||||||||||||||||||||||
![]()
|
Spécial débutant IDENTITÉ d'EULER et HYPOTHÈSE DE RIEMANN Où il
est question de relier les nombres entiers
aux nombres
premiers et d'étudier la répartition de ces nombres premiers. |
|
|
||
|
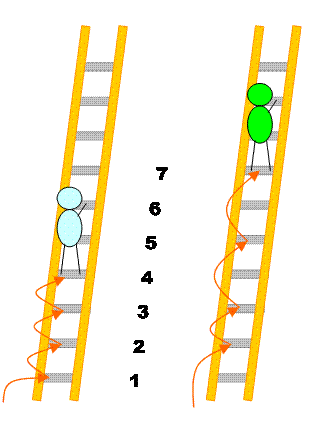
Il
y ceux qui jouent la sécurité et qui montent à l'échelle barreau après
barreau. Ce sont les nombres ENTIERS naturels Et,
il y a les sportifs qui jouent aux jeunes premiers. Ils
montent les barreaux par deux, et parfois bien davantage Ce sont les nombres PREMIERS |
|
|
|
Vers
1730, Euler observe attentivement ces
deux populations que tout oppose, et trouve curieusement une formule qui les
relie. |
||
Voir
Expression quatre à
quatre
|
DEUX MONDES QUE TOUT OPPOSE |
|
|
|
Nombres
entiers naturels 1, 2,
3, 4, 5, 6, 7 … |
Nombres
premiers 2, 3,
5, 7, 11, 13, 17 … |
|
|
|
|
|
|
|
|
|
|
5
|
5 = 1 x 5
– Nombre premier 21 = 1 x 3 x 7 – Nombre composé
|
|
|
|
||
|
UN PONT ENTRE LES DEUX MONDES |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Euler remarque (et démontre) que:
Ou, écrit autrement:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Égalité mystérieuse et magique, et ce n'est
pas fini! L'égalité est vraie pour les nombres au
carré, comme indiqué ci-dessus. Elle vraie aussi pour toutes les puissances
plus grandes des nombres: Identité
d'Euler
Identité, car l'égalité est
vraie pour toute les valeurs de s Une équation n'est vraie que pour
certaines valeurs de s, que,
généralement, on cherche à trouver. |
Inverse en anglais: reciprocal
|
|
||||||||||||||
|
|
||||||||||||||
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Identite/IdEulerD.htm
|
![]()