NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 22/11/2017 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	CONSTANTES
Débutants NOMBRES	CONSTRUCTIONS GÉOMÉTRIQUES				Glossaire NOMBRES
INDEX Nombres en représentation	Général	Fractions	Puissances	Racines
		Sommaire de cette page

Construction géométrique

des puissances

Construire les puissances
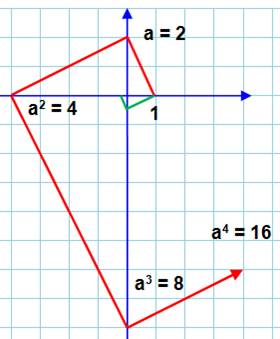
Pour construire les puissances croissantes, on trace d’abord le segment partant de (1, 0) et aboutissant à (0, a) Les perpendiculaires successives (en rouge) produisent les puissances de a. La propriété utilisée est la suivante : le carré de la hauteur (a² = 2²) est égal au produit des longueurs des segments qu’elle découpe (4 x 1). Et pour le suivant on trouve h² = 4² = 2.x, soit x = 16 /2 = 8 = 2^3. Et encore : h² = 8² = 4.x, soit x = 64 / 4 = 16 = 2^4. Etc. En vert, en tournant dans l’autre sens, on construit les inverses des puissances successives : 1/ a^n.
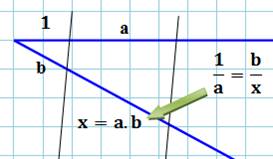
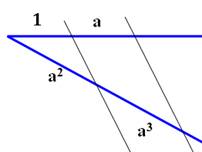
Autre possibilité en utilisant le théorème de Thalès Deux demi-droites avec les segments 1, a et b ; alors, le quatrième segment a pour mesure le produit a.b. Si a = b, alors ce quatrième segment vaut le carré de a. En portant le carré de  « a » à la place de « b », on construit aussi facilement le cube de « a ».

Suite	Construction des racines Constructions géométriques élémentaires Valeurs de racine de 2 Racine de 3 Pi Nombre d'Or
Voir	Calcul – Index Constantes Constructible Construction des carrés en couronnes de même aire (racine de 2, de 3, de 6 …) Imaginaires Racine Racine carrée Racines continues
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Nombre/ConstPu.htm