|
||||||||||||||||||||||||||||||||
![]()
|
Nombres SEMI-PREMIERS Nombres comme produit de
deux diviseurs
premiers, identiques ou différents. Exemples
|
Principaux
nombres selon la quantité de facteurs
|
ak
٠ bl ٠ cm … & ak' ٠ bl' ٠ cm'
… |
|
|
a1
٠ b1 ٠ c1 … avec
premiers ou non |
|
|
a1
٠ b1 Simple à deux facteurs |
|
|
a1
٠ b1 ٠ c1
Simple à trois facteurs |
|
|
a1
٠ b1 &
#a = #b (# est la quantité de chiffres) |
Voir détails en Types
de nombres selon leurs facteurs
|
|
||
|
Noms |
|
|
|
Définitions |
C'est
donc un nombre qui a trois (cas des carrés) ou quatre diviseurs.
|
|
|
Exemples |
6 = 2x3,
10 = 2x5, 14 = 2x7, 15 = 3x5, 21 = 3x7, 22 = 2x11, 26 = 2x13, 33 = 3x11, 34 =
2x17, 35 = 5x7 … Tous 4, 6, 9,
10, 14, 15, 21, 22, 25, 26, 33, 34, 35, 38, 39, 46, 49, 51, 55, 57, 58, 62,
65, 69, 74, 77, 82, 85, 86, 87, 91, 93, 94, 95, 106, 111, 115, 118, 119, 121,
122, 123, 129, 133, 134, 141, 142, 143, 145, 146, 155, 158, 159, 161, 166,
169, 177, 178, 183, 185, 187 … Voir OEIS
A001358 Premier
triplet de semi-premiers consécutifs. 33, 34 et
35 Plus
grand espace entre deux semi-premiers inférieurs à 1000 818 et 831 |
|
|
Anglais |
Semiprime, biprime,
2-almost-prime or pq prime. |
|
Table de multiplication des nombres premiers
=
Nombres semi-premiers
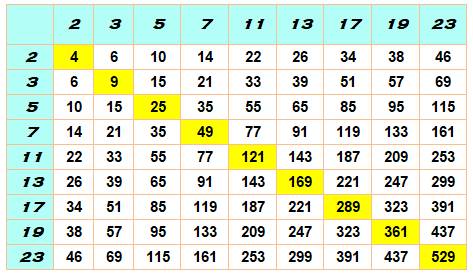
Voir Tables de multiplication / Tables de nombres – Index
Merci à Fabien T.
|
|
||
|
Simples |
|
|
|
Forme |
= 36kh + 6k + 6h +
1 = 6 (6kh + k + h) + 1 = 36kh – 6k + 6h –
1 = 6 (6kh – k + h) – 1 = 36kh + 6k – 6h –
1 = 6 (6kh + k – h) – 1 = 36kh – 6k – 6h +
1 = 6 (6kh – k – h) + 1 =
6M Comme tous les premiers, les nombres
semi-premiers sont de la forme: Pour les premiers >3 et les
semi-premiers > 9 Exemples 5005 = 6 x 834 + 1 = 35 x 143 = (6 x 6 – 1) (6 x 24 –
1) 2 692 817
= 6 x 448 803 + 1 = 391 x 6 887 = (6 x 65 – 1) (6 x 1
148 + 1) |
|
|
Famille des nombres en 6k |
Pour tout semi-premier, il est possible de trouver
deux nombres positifs k et h tels que: - Si
N = 6M + 1 alors M = 6kh + k + h ou M
= 6kh – k – h - Si
N = 6M – 1 alors M = 6kh + k – h ou M
= 6kh – k + h Exemples
(trois des solutions sur sept possibles) 5005 = 6 x
834 + 1 = 6 (6 x 2 x 64 + 2 + 64 ) + 1 5005 = 6 x
834 + 1 = 6 (6 x 6 x 24 – 6 – 24 ) + 1 5005 = 6 x
834 + 1 = 6 (6 x 11 x 13 – 11 – 13 ) + 1
|
|
|
Avancées |
|
|
|
|
||
|
Programme Maple
Version pour copier-coller dans Maple with(numtheory); SP := proc (n)
local F, q; F := `minus`(divisors(n), {1, n}); q := nops(F); if q = 2 then
return n end if end proc; {seq(SP(i), i = 10 .. 30)}; |
Commentaires Appel du
logiciel de théorie des nombres (numtheory). Procédure
SP (Semi-Premier) pour le nombre n. F
contient les diviseurs propres de n
(tous sauf 1 et n), et q donne la quantité de ces diviseurs (nops = number of
operands). Si
celle-ci-vaut 2, le nombre n est semi-premier, il est retourné vers le
programme principal. On teste
la procédure en demandant la séquence
(seq) testant les semi-premiers (SP) entre i = 10 et i = 30. Voir Programmation |
|
|
|
||
|
Les
nombres p et q sont des nombres premiers distincts. Exemples 34 = 2 x
17 = 3² + 5² 58 = 2 x
29 = 3² + 7² |
Liste jusqu'à 15 000 34, 58, 74, 146, 178, 194, 218, 298, 314, 365, 386, 458, 482, 533,
538, 554, 698, 818, 866, 965, 1082, 1202, 1322, 1418, 1538, 1658, 1685, 1706,
1853, 1858, 1874, 2018, 2042, 2138, 2218, 2234, 2258, 2498, 2642, 2813, 2818,
2858, 2978, 3098, 3218, 3338, 3506, 3578, 3602, 3746, 4058, 4178, 4322, 4442,
4538, 4562, 4682, 4778, 5045, 5354, 5378, 5498, 6002, 6245, 6338, 6362, 6602,
6722, 6893, 6898, 6914, 6938, 7058, 7082, 7418, 7538, 8042, 8258, 8522, 8882,
9098, 9458, 9578, 9602, 9722, 9818, 9938, 10226, 10562, 10618, 10898, 11042,
11138, 11162, 11282, 11378, 11402, 11453, 11474, 11498, 11642, 11738, 11885,
11906, 12242, 12458, 12722, 12773, 12778, 12794, 12842, 12938, 12962, 13058,
13418, 13562, 13658, 13682, 13898, 13922, 14138, 14258, 14618, 14738, 14978 … |
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/aNombre/TYPMULTI/SemiPrem.htm |
![]()


