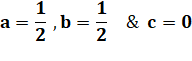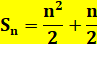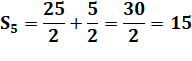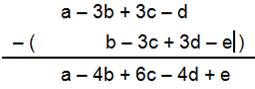|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Différences kièmes Différences finies Calcul de la différence
entre les nombres d'une suite, puis calcul de la différence entre celles-ci,
puis … jusqu'à répéter k fois cette opération: différences finies. Se dégage une relation entre
les différences kièmes et le triangle
de Pascal et même avec les factorielles. |
Anglais: Finite difference
|
|
||||
|
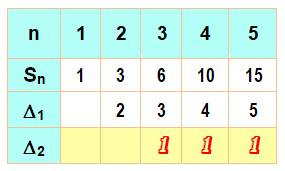
Suite de
nombres La suite
des nombres (n) et la suite Sn des nombres: Sn = Sn-1
+ n. On
calcule la différence entre les nombres (évident, bien sûr), puis la seconde
différence. Celle-ci
est constante et égale à 1. |
Suite et ses différences 1ère et 2e
|
|||
|
Théorème Si la
différence seconde est constante, la suite est représentée par une équation du second degré. Si la
différence troisième est constante, Sn est du troisième degré. |
Mise en
équation Sn
= an² + bn + c S1
= a + b + c = 1 S2
= 4a + 2b + c = 3 S3
= 9a + 3b + c = 6 |
Résolution
et vérification
|
||
Voir Résolution d'un
système d'équations
|
|
||
|
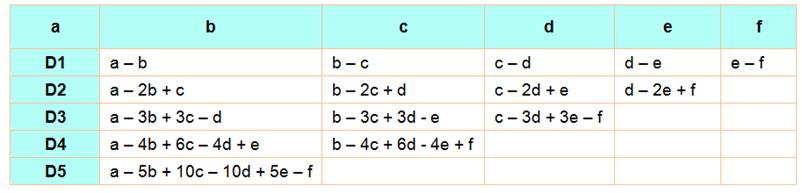
Soit une
suite de nombres: a, b, c, … Calculons
la différence entre ces nombres deux à deux et dans l'ordre. Tableau des différences kièmes
Deux types d'observations |
||
|
En horizontal Les
expressions sur une ligne sont de même forme. On passe de l'une à la suivante
en faisant glisser les lettres d'un cran. Prenons a – b et b – c. En faisant la
soustraction: a est unique; b apparaît deux fois et chaque fois avec le signe
moins; et, c vient une seule fois avec deux fois le signe moins, le
propulsant en signe plus dans la formule. Exemple de soustraction
Conclusion Pas étonnant de retrouver des sommes
algébriques qui se cumulent en donnant les coefficients du triangle de
Pascal; on dit aussi: coefficients
du binôme car, ils sont impliqués dans le développement de (a + b)n. |
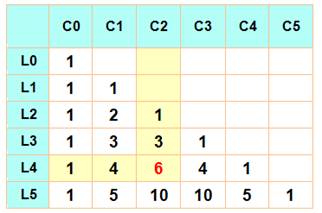
En vertical Les
coefficients sont ceux du triangle
de Pascal avec signe alterné:
Notation: Le 3e de la 4e ligne:
Rappel du calcul
La fraction commence
par les mêmes coefficients et comporte 2 facteurs (comme le 2 de C2). |
|
|
|
||
|
Reprenons
comme exemple la différence 5ième. Écriture
avec les coefficients du binôme Nommons
les a, b, c … par a0, a1, a2 … avec des
indices qui faciliteront l'écriture. Introduction
du signe de sommation et de l'indice i qui va passer par les valeurs 0 à
5. Formulation
du signe avec une puissance de -1; elle est positive pour les puissances
paires. Généralisation
à la différence de rang k. |
|
|
|
|
||
|
Soit une
suite de nombre n, n – 1, n – 2, n – 3, … Calculons
la différence entre ces nombres deux à deux: sans intérêt! ce sont des
nombres consécutifs. Par contre prenons le carré de ces nombres ou la
puissance p de ces nombres. Nous
retrouverons évidemment les propriétés énoncées ci-dessus. Elles sont à la
base du fonctionnement de la machine à calculer de Babbage. |
||
|
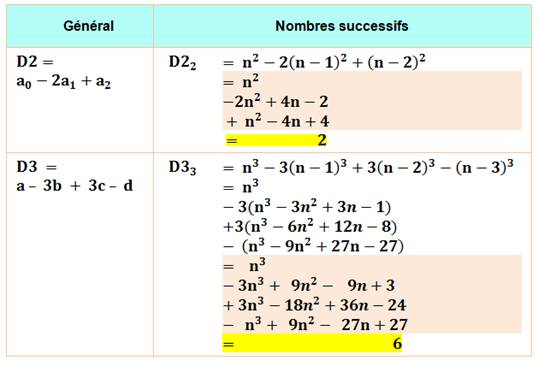
La formule générale pour la deuxième différence
est rappelée en colonne "général"; de même que celle pour la
troisième différence. Remplaçons: a0, a1, a2
… par les nombres consécutifs n, n – 1, n – 2 … En haut, nous portons ces nombres au carré et
calculons la différence deuxième D22. En bas, la différence troisième avec les cubes. Résultat incroyable! |
|
|
|
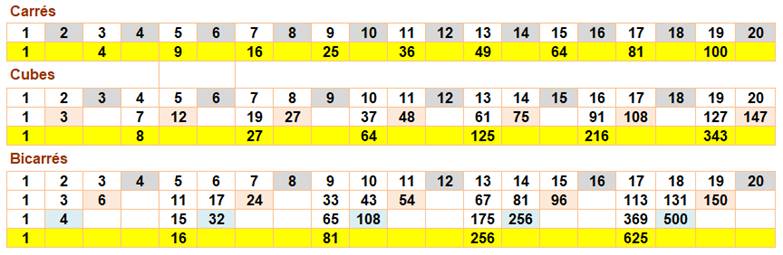
Carrés |
La différence deuxième entre carrés de nombres successifs est constante et
égale à 2. |
|
|
Cubes |
La différence troisième entre cubes de nombres successifs est constante et
égale à 6. |
|
|
Puissance
k |
La différence kième entre la
puissance kième de nombres successifs est
constante et égale à k!. |
|
Un truc pour le calcul de puissances
|
Pour
trouver la suite des carrés:
Pour
trouver la suite des cubes:
|
Voir Brève
48-957
![]()
|
Suite |
|
|
Voir |
|
|
Cette
page |