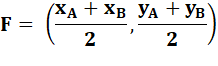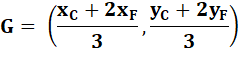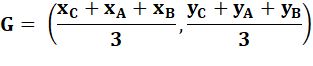Médianes concourantes

Édition du: 31/08/2022

INDEX Types de triangles Triangle Géométrie	Triangle: Droites remarquables
	Droites et points	Bissectrices	Médianes – Propriétés (1)
	Point Milieu	Médiatrices	Médianes – Partage (2)
	Point et triangles	Hauteurs	Médianes – Démo (3)
	Distances	Triangle médian	Médianes – Démo vecteurs (4)
	Céviennes régulières		Médianes – Démo autres (5)

MÉDIANES du TRIANGLE (3/5)

Démonstrations

Démonstrations à propos des médianes des triangles et de leur point de concours, le centre de gravité.

Sommaire de cette page

>>> Types de démonstrations

>>> Démonstrations

Débutants

Géométrie

Glossaire

Médianes

Triangle

Voir Propriétés fondamentales des triangles

Démonstrations – Type et Accès

Géométrique	Longueurs 2:1 >>> Céviennes >>> Parallélogramme >>> Trapèze >>> Triangles semblables >>> Droites parallèles >>>
Analytique	Coordonnées du centre de gravité >>>
Calculs	Proportions >>> Calcul des aires >>>
Logique	Descente infinie >>>
Vecteurs	Calcul vectoriel >>> Vecteurs à somme nulle >>> Isobarycentre >>>

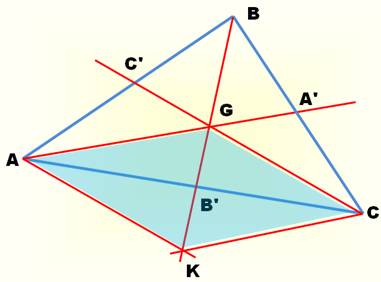
Démo – Parallélogramme (Démo classique et simple)		haut
Hypothèses Un triangle ABC; AA' et CC' deux médianes qui se coupent en G. La droite BG coupe AC en B'. Ce qu'il faut démontrer AB' = B'C et alors la droite BB' est la troisième médiane. Démonstration Construire le point K symétrique de B par rapport à G.
Diagonales	BG = GK Il faut démontrer que B' est le pied de la médiane. Ce sera le cas si GK et AC sont les diagonales d'un parallélogramme.
Parallèles Théorème du point milieu	Dans le triangle BAK, C' et G sont des points milieux: C'G est parallèle à AK. Dans le triangle BCK, A' et G sont des points milieux: A'G est parallèle à CK.
Parallélogramme	Avec des côtés parallèles deux à deux, le quadrilatère AGCK est un parallélogramme.
En prime	BG = GK = 2GB' ou encore GB' = 1/3 BB'

VARIANTE	Construire en C la parallèle à AA' qui coupe BB' en K.
Dans le triangle BCK,	A' étant le milieu de BC et A'G est parallèle à CK, Alors, G est le milieu de BK.
Dans le triangle ABK,	G et C' sont les milieux des côtés, Alors, C'G est parallèle à AK.
Le quadrilatère AGCK	Il a ses côtés parallèles deux à deux, c'est un parallélogramme.
Ses diagonales se coupent en leur centre:		AB' = B'C.

Démo – Longueurs 2:1		haut
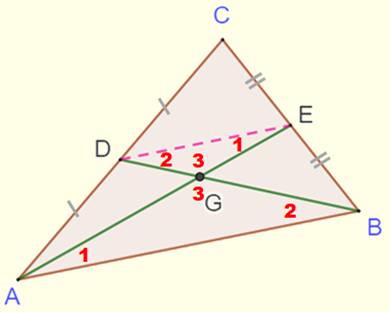
Hypothèses Triangle ABC Médianes AE et BD; intersection en G. Ce qu'il faut démontrer Le point G est unique pour toutes les médianes prises deux à deux. Idée Proportions dans les triangles semblables AGB et EGD. Le point G découpe une paire de médianes dans la proportion 2 : 1. Avec une autre paire, on a le même point G. On en déduit que le point G est unique.
DE parallèle à AB	Les points D et E sont les milieux de AC et BC, les droites DE et AB sont parallèles. Les triangles CDE et CAB sont semblables: AB = 2DE
Triangles AGB et EGD	Avec des angles égaux (en rouge), les triangles AGB et EGD sont semblables. AB / DE = AG / GE AG = 2 GE
Suite …	Cette proportion est valable pour la deuxième médiane pour le même point G. On recommence avec une autre paire de médianes pour constater que le point G est le même.

Démo – Théorème de Céva

haut

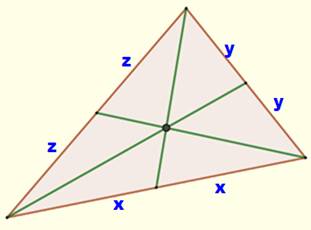
Hypothèses

Un triangle ABC et ses médianes.

Les demi-longueurs des côtés x, y et z.

Théorème de Céva

Condition nécessaire et suffisante pour que les trois céviennes soient concourantes:

Ce qui est le cas ici.

Démo – Trapèze		haut
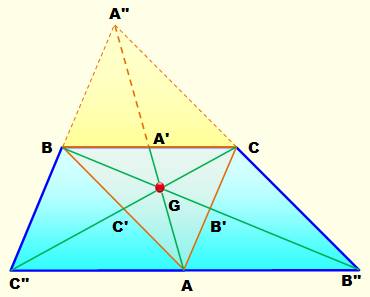
Construction Triangle ABC. Construction du triangle dont ABC sera le triangle médian: C''B'' parallèle à BC en A. BC'' parallèle à AC en B. CB'' parallèle à AB en C. Idée Le point G est le point de concours des diagonales et médiane du trapèze. Ce point est aussi le point de concours des médianes des triangles ABC et A''B''C''. Identification de parallélogrammes et de triangles isométriques.
Avec deux côtés parallèles:	Le quadrilatère BCB''C'' est un trapèze.
Avec leurs côtés parallèles deux à deux:	Les quadrilatères BCAC'' et BCB''A sont des parallélogrammes, et BC = C''A = AB''. Les diagonales se coupent en leur milieu: BC' = C'A et CB' = B'A BB' et CC' sont les médianes du triangle ABC.
Du fait du tracé des parallèles:	Les quatre triangles de cette figure (ABC, A"BC, BAC'' et CAB"") ont des angles égaux et un côté de même mesure. Ils sont isométriques (superposables directement ou par rotation).
Avec BC = C''A = AB'', A est le milieu de C''B" Avec BC parallèle à B''C'', le point A' est le milieu de BC.	La droite AA' est la médiane du trapèze BCB''C''.
Avec A''B = BC'' et A''C = CB":	Les diagonales CC'' et BB'' du trapèze sont aussi les médianes du triangle A''B''C''.
Théorème du trapèze Dans le trapèze, les diagonales BB'' et CC''et la médiane AA' se coupent en un point unique G.	Les médianes du triangle ABC se coupent en un point unique G. Les médianes du triangle A''B''C'' se coupent en un point unique G.

Démo – Triangles semblables		haut
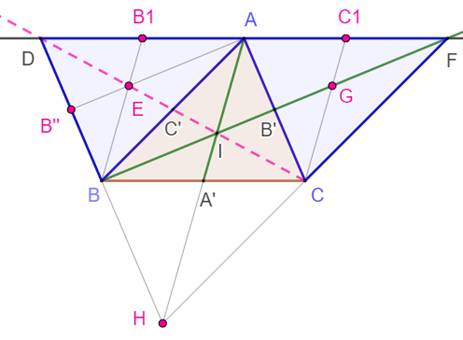
Construction Triangle ABC. Parallèles aux côtés opposés formant le triangle DFH. Deux médianes AA' et BB' (en vert) avec intersection en I. Il s'agit de montrer que la troisième médiane CC' passe par I. Construction complémentaire Médianes BB₁ et CC₁ des triangles bleux. Diagonale BF. Diagonale DC. Droite AE qui coupe DB en B''.
En bref	Cette démonstration reprend celle avec le trapèze, en ignorant le théorème du trapèze Les triangles colorés étant superposables, si le point G ou E est un point de concours des médianes, alors le point I l'est aussi. Deux médianes dans chaque triangle bleu, par superposition de ces triangles, produisent les trois médianes qui se coupent en un même point.
Triangles isométriques	Avec l'effet des parallèles, les quadrilatères DACB et AFCB sont des parallélogrammes: BC = DA = AF. Les angles des triangles ABC, BAD et CFA sont égaux deux à deux, et avec un côté de même mesure, ils sont isométriques (égaux).
EB₁ = GC₁	A milieu de DF; B₁ milieu de DA et C₁ milieu de AF. B₁A = AC₁ = BA' = A'C. AA', BB₁ et CC₁ sont parallèles. AA' = BB₁ = CC₁. Dans le triangle DCC₁: le point B₁ est situé au 1/3 de DC₁. Avec Thalès: EB₁ = 1/3 CC₁ Même chose avec le triangle FBB₁ et GC₁ = 1/3 BB₁. En rapprochant les deux égalités: EB₁ = GC₁
Superposition	Dans le triangle de droite (AFC), deux médianes se coupent en G. On superpose le triangle de droite sur celui de gauche, y compris ses attributs: CC₁ en BB₁; G en E; FB' en AB". Le point B' est le milieu de AC; B" est donc le milieu de DB. Le point E, construit comme intersection de BB₁ et DC est également sur la médiane AB".
DC' est médiane	Dans le parallélogramme DACB, les diagonales se coupent en leur milieu: le point C' est le milieu de AB et DC' est la troisième médiane de DAB. Les trois médianes de DAB se coupent au même point E. C'est le cas pour ses triangles semblables ABC et ACF.
Centres de gravité	Cette figure montre que le point I est le centre de gravité des triangles ABC et HDF. Et, que E et G sont les centres de gravité des triangles DAB et AFC.

L'idée de cette démonstration est due à Rachid Annouaoui

Démo –Coordonnées		haut
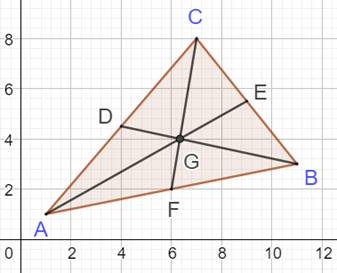
Repère Oxy. Coordonnées des points (x_i, y_i). Idée On suppose que le point G est situé au 2/3 de chaque médiane. On montre que les trois couples de coordonnées obtenues sont identiques et, donc, que le point G est unique.
F milieu de AB
G au 2/3 de CF
Avec les coordonnées de F
Formule symétrique en A, B et C	Les coordonnées de A, B et C peuvent être permutées sans changer les coordonnées de G. Un calcul sur les deux autres médiatrices donnerait le même résultat. Le point G est unique.

SUITE Démonstrations avec vecteurs (3/4) >>>

Haut de page

Retour	Médianes – Propriétés Droites et points
Suite	Médianes concourantes – Démonstrations avec vecteurs Illustration en 3D du centre de gravité d'un triangle Construire le triangle connaissant les médianes Quatre triangles Triangles et carrés Triangles et droites de partage
Voir	DicoMot DicoNombre Droite de Simson Droite d'Euler Éléments de géométrie	Triangle – Débutants, novices Médianes – Glossaire Triangle – Index Cercle Losange et son cercle inscrit
Sites	Médianes dans un triangle – Comme exercice de 4^e (avec le formalisme requis) Point de concours des médianes – Bibm@th Les médianes d’un triangle – Questions types du bac The Medians – Cut-The-Knot – Preuve par descente infinie Proof That the Medians of a Triangle are Concurrent – Michael McCallum Concurrence of Medians (1 of 2: Proof via similar triangles) – Eddie Woo - Vidéo
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Propriet/Mediane1.htm

Haut de page