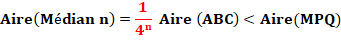|
Édition du: 31/08/2022 |
|
INDEX |
Triangle:
Droites remarquables |
||
|
Médianes – Propriétés (1) |
|||
|
Médianes – Partage (2) |
|||
|
Médianes – Démo (3) |
|||
|
Médianes – Démo vecteurs (4) |
|||
|
Médianes – Démo autres (5) |
|||
![]()
|
MÉDIANES du TRIANGLE (5/5) Démonstrations Démonstrations
à propos des médianes des triangles
et de leur point de concours, le centre
de gravité. |
||
|
|
Sommaire de cette page >>>
Démo – Calculs d'aires >>>
Démo – Descente infinie >>>
Démo – Proportions >>>
Démo – Droites parallèles |
Débutants Glossaire |
Voir Propriétés fondamentales
des triangles
|
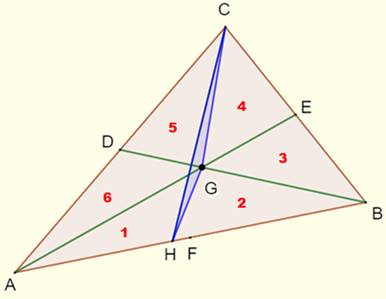
Construction Triangle ABC. Les médianes AE et BD; intersection
en G La troisième médiane CH volontairement dessinée
ne passant pas par G et créant une surface interne CGH Le but est de démontrer que son aire est nulle. Une médiane partage un triangle en deux triangles
de même aire. Les trois médianes le partagent en six triangles
de même aire (notés de 1 à 6). |
|
||
|
Aires Le soulignement indique
qu'il s'agit des aires |
ACH + CHG + CGHB = ABC = 1 (comme référence) |
||
|
Aire de ACH |
CH est la médiane du triangle ABC: ACH = BCH
= 1/2 CHG + CGHB
= 1/2 |
||
|
Aire de CGHB |
CGHG = 2 + 3 + 4 = 3 x (1/6) = 1/2 |
||
|
Aire de CHG |
CHG + 1/2 =
1/2 CHG = 0 |
||
|
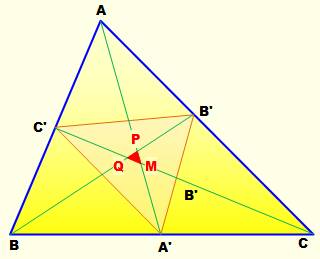
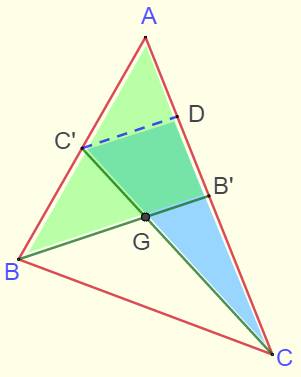
Construction Triangle ABC. Médianes AA', BB' et CC' Hypothèse Les trois médianes ne sont pas concourantes. Elles créent un petit triangle intérieur MPQ. Idée Tous les triangles
médians successifs ont les mêmes médianes et l'aire de chacun est égale à
1/4 du triangle mère. Démonstration Lors de la création de tous les triangles médians
successifs, les médianes sont invariantes et, avec elles, le triangle MPQ. Or, ce triangle reste interne au triangle qui le
crée. L'aire du triangle médian est égale à 1/4 de
celle du triangle mère. L'aire du triangle MPQ reste inférieure à
celle-là. |
Mise en évidence du triangle
hypothétique MPQ
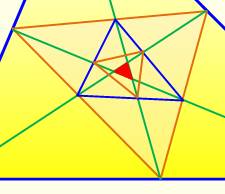
Zoom sur les triangles médians
successifs
|
||
|
Au rang n: |
|
||
|
Quand n tend vers l'infini: |
|
||
|
Construction Triangle ABC. Médianes BB' et CC'. Parallèle C'D à BB'. Idée Propagation de proportions via les triangles
semblables colorés. Démonstration Les triangles ABB' et AC'D sont semblables. Alors: B'D = 1/3 CD. Les triangles CDC' et CB'G sont semblables. Le point G est sur la médiane CC' au 1/3 de la distance. Avec la médiane AA' (au lieu de BB'), on
trouverait que le point K est au 1/3 de CC',
dit autrement K et G sont confondus. G
est unique. |
|
|
|
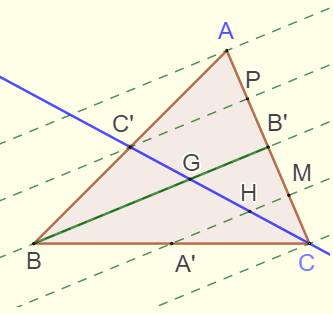
Construction Triangle ABC. Point B' milieu de AC. Parallèles en ces points à BB'. Droite CC'. Idée Si une sécante coupe des parallèles selon des
segments égaux, toute autre sécante en fera autant. Démonstration |
|
||
|
Sécante AC: |
Segments égaux: AP = PB' = B'M = MC |
||
|
Conséquence sur sécante CC': |
Segments égaux: C'G = GH = HC |
||
|
Triangle ABB': |
Le point P est le milieu de AB' C'P // BB' Le point C' est le milieu de AB. CC' est une
médiane. |
||
|
Point G: |
Le point G est le point de concours de deux
médianes (BB' et CC'). |
||
|
Autres faisceau de parallèles |
Même raisonnement avec une autre série de
parallèles qui donne le même pont G. |
||
|
En prime |
G est situé au 2/3 de CC' en partant du sommet
C. |
||
RETOUR médianes – Démos >>>
![]()
|
Retour |
|
|
|
Suite |
|
|
|
Voir |
|
|
|
Sites |
|
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Propriet/Mediane3.htm
|
|