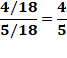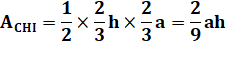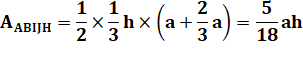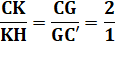Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 14/10/2023 M'écrire Brèves de Maths

INDEX Types de triangles Triangle Géométrie	Triangle: Droites remarquables
	Droites et points	Bissectrices	Médianes – Propriétés (1)
	Point Milieu	Médiatrices	Médianes – Partage (2)
	Point et triangles	Hauteurs	Médianes – Démo (3)
	Distances	Triangle médian	Médianes – Démo vecteurs (4)
	Céviennes régulières		Médianes – Démo autres (5)

MÉDIANES du TRIANGLE (2/5)

Quelques propriétés remarquables des médianes des triangles et le centre de gravité.

On trouvera d'autres propriétés lors de l'exploration des démonstrations sur les pages suivantes.

Les trois médianes d'un triangle se rencontrent en un point unique, le centre de gravité du triangle.

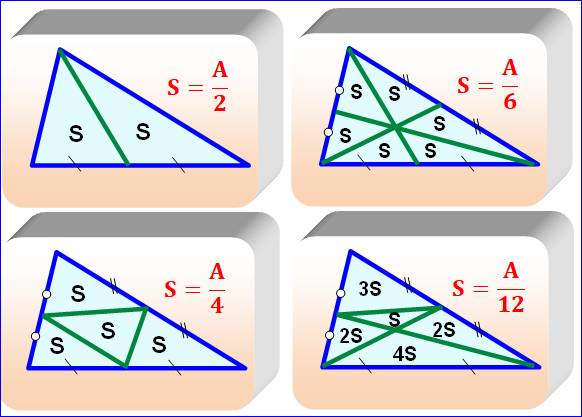
Chaque médiane partage le triangle en deux triangles de même aire.

Les trois médianes partagent le triangle quelconque en six triangles de même aire.

A savoir Dans le triangle quelconque

Sommaire de cette page

>>> Médianes et partage

>>> Triangles de même aire

>>> Proportion 2 : 1

Débutants

Géométrie

Glossaire

Médianes

Triangle

Voir Propriétés fondamentales des triangles

Résumé concernant le partage des triangles quelconques par les médianes

Voir Brève 54-1079

Médianes et partage		haut
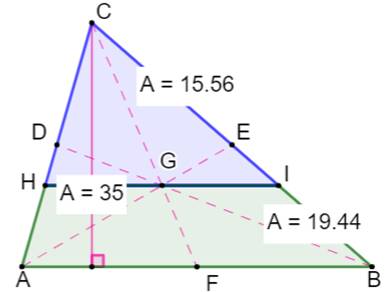
Propriétés Les médianes se coupent en un point unique, le centre de gravité G. Notez que la distribution naturelle des lettres pour les sommets et les milieux des côtés aboutit à la lettre G pour le nouveau point. Coïncidence ! CG = 2/3 CF et FG = 1/3 CF. La médiane partage le triangle en deux triangles de même aire.	Aire du triangle: 1/2 x 10 x 7 = 35 Aire du triangle: 2/9 x 10 x 7 = 15,555… Aire du trapèze: 5/18 x 10 x 7 = 19,444…
Calculs des aires Avec la parallèle HI à AB, le triangle CHI occupe une surface égale aux 4/5 de celle du trapèze ABIH.
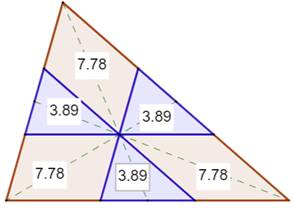
Surfaces de mêmes aires Cette proportion est valable pour les trois médianes: les trois triangles au sommet sont égaux comme le sont les trois trapèzes. Par comparaison, on établit que tous les triangles bleus ont la même aire, de même que tous les parallélogrammes ocres.	Mêmes dimensions que ci-dessus (triangle 10 x 7)

Voir Brève 720

Triangles de même aire		haut
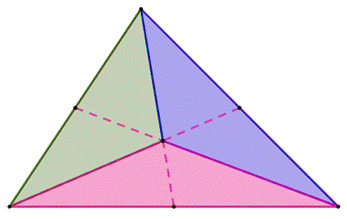
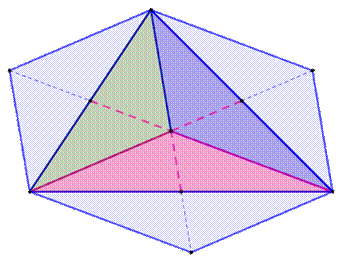
Un triangle quelconque. Ses trois médianes. Elles partagent le triangle en trois triangles (vert, bleu et rose) de même aire égale à 1/3 de l'aire du triangle initial. Chacun de ces triangles est partagé en deux triangles de même aire par la "queue" des médianes (base de même longueur et sommet commun). Leur aire est égale à 1/6 de l'aire du triangle initial.	Les SIX petits triangles ont la même aire.
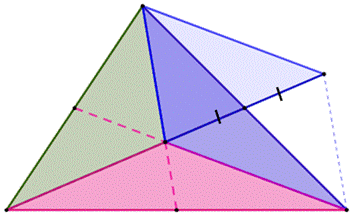
La même figure. Une des médianes est prolongée de la même longueur que sa "queue" (soit 1/3 de la médiane complète). Le quadrilatère obtenu en dessinant le pointillé bleu est un parallélogramme (diagonales qui se coupent en leur milieu). Les côtés opposés sont parallèles. Les deux triangles bleus ont même base et leur sommet est situé sur une parallèle à la base; ils ont la même aire. Soit 1/3 de l'aire du triangle initial.	Les HUIT petits triangles ont la même aire.
Pour l'amusement, complétons le triangle par les trois triangles périphériques tels que vus ci-dessus. La figure obtenue est un octogone dont les côtés opposés sont parallèles et égaux deux à deux. Son aire est deux fois celle du triangle initial. En bleu clair, voyez-vous le pavé droit (parallélépipède). Les trois triangles foncés forment un trièdre posés sur trois faces de ce pavé.	Vue perspective d'un pavé droit.

Proportion 2 : 1
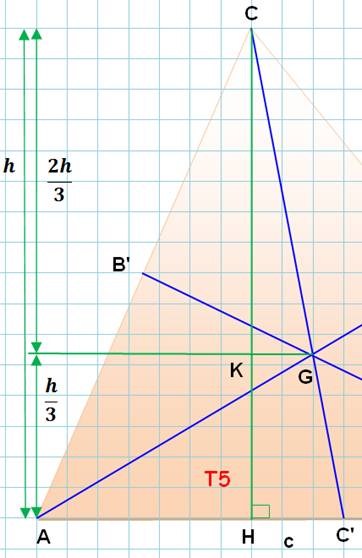
Nous savons que le centre de gravité G, point de concours des médianes, est tel que GC' = 2GC. En vert, la hauteur CH et la parallèle GK à la base AC' en G. Théorème de Thalès: Aires des triangles: Dans un triangle quelconque, une médiane découpe le triangle latéral à une médiane en deux triangles dont l'un est le double de l'autre.	Aire AGC = 2 Aires AGC'

Retour à Triangle quelconque

Haut de page

Retour	Droites et points Médianes
Suite	Médianes concourantes – Démonstrations Illustration en 3D du centre de gravité d'un triangle Construire le triangle connaissant les médianes Quatre triangles Triangles et carrés Triangles et droites de partage Triangle médian
Voir	DicoMot DicoNombre Droite de Simson Droite d'Euler Éléments de géométrie	Triangle – Débutants, novices Médianes – Glossaire Triangle – Index Cercle Losange et son cercle inscrit
Sites	Médianes – Wikipédia Encyclopedia of triangle centers (ETC) – Tous les centres du triangle possibles et imaginables (plus de 400!) Vergessene Sätze am Dreieck (Teil 2) – Matroids Matheplanet Théorème de Stewart – Wikipédia
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Propriet/Mediane4.htm

Haut de page