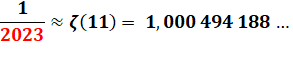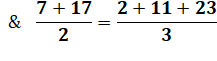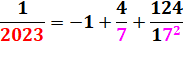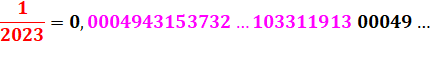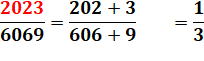Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 27/12/2023 M'écrire Brèves de Maths

DicoNombre Débutant Glossaire Types de nombres Nombres géométriques Nom des nombres Écriture des nombres Table des facteurs Nombres et anglais Langues	Dictionnaire des Nombres
	1 / 10 / 50 / 100 / 500 / 1000 / 1500 / 1900 / 2000 / 2016 / 2017 / 2018 / 2019 / 2020 / 2021 / 2022	2023	2024 / 2025 à 2099 / 3000 / 5000 / 10 000 / 20 000 / 50 000 / 100 000 / 10^6 / 10^9 / 10^100 Autres

Nombre 2023	Actualités	Humour 2022-2023
	Chiffres de 2023 (jeu)	Énigmes virales

Faites un double-clic pour un retour en haut de page

Carte d'identité du nombre

Nombre strobogrammatique

Voir Orthographe des nombres / Nombres et langues

Facteurs
Diviseurs	1, 7, 17, 119, 289, 2023
Quantité	6
Somme	2456
S - N	433
Binaire	111 1110 0111
Romain	MMXXIII

Suite en propriétés arithmétiques

Voir Année 2023

Chanceux d'Ulam

Chanceux de Josèphe (prochain: 2161)

Composé

Congruent

Déficient

Harshad

Harshad à Q-carré

Jonction (avec 1997 et 2015)

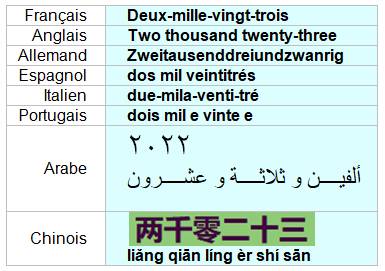
Voir Nom des nombres

Heptagonal concentrique

Nombres géométriques

Chiffres et Numération

2023 + (2+0+2+3) = 2030		Mêmes jeu de chiffres dans le nombre augmenté de ses chiffres.
2023 + 3202 = 5225 2310 = 327 23 + 32 = 55		Devient palindrome en lui ajoutant son retourné. Curiosités ave le nombre 23.
202 × 3 = 606		Palindrome avec un produit de ses chiffres.
202310 = 7E716 = [7, 14, 7]16 = 7 × 16² + 14 × 16 + 7		Palindrome en base 7 >>>
202310 = [17, 17]118 = 17 × 118 + 17 = [ 7, 7]288 = 7 × 288 + 7		Brésilien car repdigit en bases 118 et 288 >>>
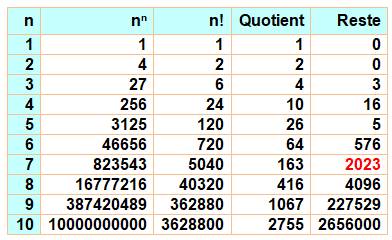
2023 = 7 × 17² => 717 et 71717		Ses facteurs forment deux palindromes. Le second en développant le carré.
2023 = 7 × 17² 2 + 0 + 2 + 3 = 7	Autant de chiffres dans le nombre et sa factorisation. Divisible par la somme de ses chiffres. La somme de ses chiffres est égale à son plus petit facteur.
2023 = (2+0+2+3) × (2²+0²+2²+3²)² = (2^7 + 0^7 + 2^7 + 3^7) ➝ 2443 – (2^5 + 0^5 + 2^5 + 3^5) ➝ 307 – (2^4 + 0^4 + 2^4 + 3^4) ➝ 113		Produit de la somme des chiffres avec la somme des carrés des chiffres au carré. Suivants: 2400, 52215, 615627, … Les deux sommes sont les facteurs du nombre (Voir ci-dessous). Rare avec un "3" pour unité. A306701 Voir Nombres narcissiques de Keith

Fantaisie exceptionnelle avec la somme de ses chiffres

(2023 – 2 – 0 – 23) / 2 = 999		Devient repdigit avec opération sur ses chiffres.
2 023 0, 2, 3, 20, 22, 23, 30, 32, 202, 203, 220, 223, 230, 232, 302, 320, 322, 2023, 2032, 2203, 2230, 2302, 2320, 3022, 3202, 3220		Les 26 nombres formés avec les chiffres de 2023. En rose les quatre nombres premiers.
2, 3, 23, 223, 2203 et 22003		Ces six nombres à motif sont premiers.
2 02 3	Trois nombres premiers en coupant le nombre.
20 23	Nombre concaténé avec le prochain nombre premier.
2 02310 = 1332134	Nombre premier en base 4.

Addition

2 023 = 43 + 44 + … + 76	Une des cinq sommes de nombres consécutifs >>>
2 023 = 103 + 104 + … + 135 = 283 + 285 + … + 295	Sommes de nombres impairs consécutifs.
2 023 = 181 + 1661 + 181 2 023 = 999 + 5 × 5 + 999	Opérations palindromiques avec palindromes.
2 023 = T2 + T3 + … + T22	Somme de nombres triangulaires consécutifs.
		Valeur proche de l'inverse de zêta (11).
2 023 = 2 + 919 + 1102 (2, 919, 2011) 2 023 = 151 + 931 + 941 (151, 139, 149) 2 023 = 35 + 994 + 994 (53, 499, 499)		Somme de trois nombres premiers retournés de multiples fois.
			Somme palindrome avec nombres stobogrammatiques - Taneja

Multiplication, division

2023 = 7 × 17²	Nombre composé avec aucun facteur autre que 1 ou 7. Précédent: 1331 = 11^3 ; Suivant: 2057 = 11² × 17
2023 = 7^1 × 17^2	Nombre tel que sa factorisation présente des exposants successifs strictement croissant. Précédent: 1944 = 2^3 × 3^5; Suivant: 2250 = 2 × 3^2 × 5^3. Avec ses exposants, on calcule la quantité de diviseurs: (1 + 1) (2 + 1) = 6
div(2023) = {1, 7, 17, 119, 289, 2023} 1 × 7 × 17 × 119 × 289 = 4 092 529 = 2023²		Le produit des diviseurs propres est égal au carré du nombre.
		Ses facteurs premiers sont les deux plus petits nombres premiers longs. Voir 1/2023 et sa période

2023 = 7 × 17² 2024 = 2² × 506 2025 = 5² × 81	Trois nombres successifs à facteurs carrés.
2023 = 7 × 17² 2024 = 2^3 × 11 × 23	Égalité de la moyenne des facteurs pour deux nombres consécutifs. Deuxième cas après 459. Suivants: 5063, 11111, 87615, 92080, 224720, …
2 022 / (2+0+2+2) = 337 2 023 / (2+0+2+3) = 289 2 024 / (2+0+2+4) = 253 2 025 / (2+0+2+5) = 225	Membres d'une chaine de quatre Harshad consécutifs. Liste des têtes de série: 510, 1014, 2022, 3030, 10 307, 12 102, 12 255, 13 110, …
2 023 = 17² × 7 2 024 = 2^3 × 253 2 025 = 3^4 × 25	Trois nombres consécutifs avec facteur, carré, cube puis bicarré. Liste: 350, 1375, 2023, 11150, 11374, 12446, 13310,
2023 / 7 = 289 7 / 7 = 1	Harshad à quotient carré: divisible par 7 comme la somme de ses chiffres. Précédent: 1974 et suivant: 2093
2023 ≡ 7^7 mod 7! 2 023 ≡ (2 + 0 + 2 + 3)^2+0+2+3 mod (2+0+2+3)		Reste de la division de n^n par n!
2023 nombres premiers consécutifs		à partir de: 8132581734 1203028233 6987547007 Plus petit cas. Voir Prime Curiosity 2023

Avec les puissances

Racine de 2023 somme de deux racines

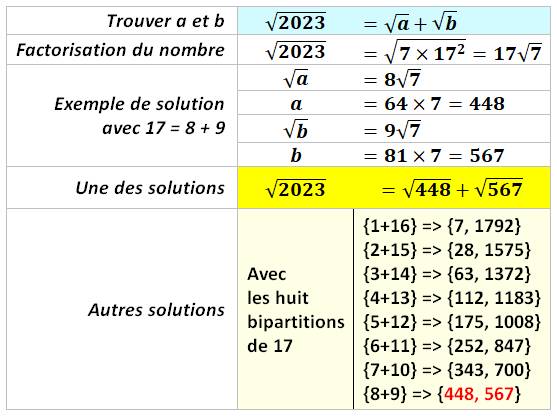
Note: solution toujours possible dès que le nombre contient un carré dans sa factorisation
Avec 2025 = 3⁴ × 5² , il ya 22 solutions

Voir Facteurs des nombres entre2020 et 2030

2023 = 4 × 22² + 4 × 22 – 1	Trois nombres successifs à facteurs carrés.
2023 = 19² + 19² + 25² + 26²	Nombreuses sommes de quatre carrés (aucune à moins de termes) >>>
2023 = 16^1 + 26^2 + 11^3 = 6^1 + 17^2 + 12^3 = 26^2 + 11^3 + 2^4 2023 = 5^1 + 3^2 + 9^3 + 4^4 + 4^5 = 6^1 + 5^2 + 7^3 + 5^4 + 4^5 = 10^1 + 2^2 + 9^3 + 4^4 + 4^5	Sommes de puissances successives à trois et quatre termes.
2023 = 7 × 17² 7 = 0^3 + (–1)^3 + 2^3 17 = 1^3 + 2^3 + 2^3+ 2023 = 2^3 + (–9)^3 + 14^3	Somme de trois cubes comme le sont ses facteurs. Est-ce que tout nombre est somme de trois cubes ? Problème ouvert. Le plus petit non connu est 114.
2023 = 14^3 + 15^3 + (–16)^3 = 6119 – 4096	Autre solution pour trois cubes. Coquetterie: trois nombres consécutifs.
2023 = 0^2 + 1^5 – 2^3 + 3^6 + 4^1 + 5^0 + 6^4		Somme de puissances et nombres successifs de 0 à 5 – Taneja
2023 = 2^3 + 5^3 + 6^3 + 7^3 + 11^3		Somme de cinq cubes.
2023 = 9^3 + 8^3 + 7^3 + 6^3 + 5^3 + 4^3 + 3^3 + 2^3 – 1^3 2025 = 9^3 + 8^3 + 7^3 + 6^3 + 5^3 + 4^3 + 3^3 + 2^3 + 1^3			Somme de cubes avec tous les nombre de 1 à 9.
2023 = 2048 – 25 = 2^11 – 5^2 = 2^5^×^2 × 2 – 5^2			Comment arriver à exprimer le nombre avec ses chiffres.
2023 < 2025 = 45²	Plus petit impair juste inférieur à un carré. Précédent: 1935 < 44²; Suivant: 2115 = 46².

En puissance

= 17 × 2,64575… = 44,977772288…		Racine carrée simplifiable. Proche de 45 (45² = 2025)
				Les neuf seuls triplets de Pythagore: {a, b, c} avec 2023. Le nombre g est le PGCD des trois nombres, lequel conduit au triplet primitif: {a', b', c'}.
10^2023 + 49	Un des nombres premiers de cette famille 1, 2, 3, 5, 8, 17, 24, 32, 65, 66, 67, 79, 83, 98, 152, 260, 781, 1225, 1777, 2023, 2411, 3469, 5347, … OEIS A108054
2023^3 / (2+0+2+3) = 34 391²	Cube divisé par somme des chiffres = carré.
2023^6 = 1902^6 + 1548^6 + 1320^6 + 1136^6 + 345^6 + 240^6 + 30^6 = 68544923587844151889 = 6,8…10^19			Sa puissance sixième est une somme de puissances sixièmes. Jean-Charles Meyrignac en 1999

Autour du nombre

a = 2023 × 6^48 – 1 b = 2023 × 6^48 + 1	Deux nombres premiers jumeaux. a = 45420917341978269296696428103432581152767 b = 45420917341978269296696428103432581152769 2023 est le plus petit coefficient pour 48; les suivants est 2930, 4420, …
		Inverse exprimé en fractions avec ses propres facteurs.
			Son inverse a une période de 816 chiffres. Voir Premiers longs

Période de 1/2023 – 816 chiffres par groupe de 50

En jaune les chiffres triplés (tous y sont de 0 à 8).

Les chiffres [2, 0, 2, 3] ne sont jamais présents.

Dénombrement, jeux et curiosités

Petite interrogation à propos de 2023 et 2024

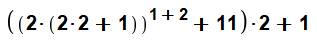
8 = 2 + 0! + 2 + 3 9 = (2 – 0! + 2) × 3 10 = 2 + 0 + 2 + 3!			Faire tous les nombres successifs avec les quatre chiffres de 2023.
2023 = 12 × 3 × (4 + 5) × 6 + 7 + 8 × 9 = 9 × 8 + 7 + 6 × 54 × 3 × 2 × 1 = (10 – 9) (8 – 7 + 6)(5 + 4 ×3)² × 1				Opérations pannumériques
2023 =	= ((10)^3 + 11) × 2 + 1 = 1011 × 2 + 1			Faire 2023 avec des "1" et des "2".
2023 = 1×2 + (3!)^4 + 5 + 6! = 2 + 1296 + 5 + 720		Faire 2023 avec le minimum de chiffres successifs – Alain Zalmanski
2023 = (–1 + 234 + 56) × 7		Faire 2023 avec le minimum de chiffres successifs – François Lavallou
		Fraction avec les mêmes chiffres au numérateur et au dénominateur. Taneja
1, 3, 10, 20, 22, 31, 32, …, 2023			Membre de la suite des nombres pointant vers les "1" de la même liste.
1, 2, 3, 4, 7, 41, 43, 47, … 2023			Membre de la suite des nombres tels que la somme de deux chiffres successifs est un nombre premier.
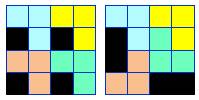
2023	Quantité de façons de paver un carré 4×4 en utilisant de 1 à 4 fois le triomino en L. Voir Number 2023 – Numbers Aplenty			Deux exemples de tels pavages

Faire 2023 avec plusieurs fois le même chiffre

Voir Nombre 2020 en chiffres

D'après Single Digit Representations of Numbers From 1 to 2500 – Inder J. Taneja

Calendrier

2023 est une année à 53 dimanches (en non 52). Le 1^er janvier 2023 est un dimanche. Dans le cas d'une année bissextile, le 1^er janvier peut être aussi un samedi. On a eu 53 dimanches en: 2000, 2006, 2012 et 2017.

>>>

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération: base, [chiffres]			Repdigit (Brésilien)
2, [1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1] 3, [2, 2, 0, 2, 2, 2, 1] 4, [1, 3, 3, 2, 1, 3] 5, [3, 1, 0, 4, 3] 6, [1, 3, 2, 1, 1] 7, [5, 6, 2, 0] 8, [3, 7, 4, 7] 9, [2, 6, 8, 7] 10, [2, 0, 2, 3] 11, [1, 5, 7, 10]	12, [1, 2, 0, 7] 13, [11, 12, 8] 14, [10, 4, 7] 15, [8, 14, 13] 16, [7, 14, 7] 17, [7, 0, 0] 18, [6, 4, 7] 19, [5, 11, 9] 20, [5, 1, 3] 21, [4, 12, 7]	22, [4, 3, 21] 23, [3, 18, 22] 24, [3, 12, 7] 25, [3, 5, 23] 26, [2, 25, 21] 27, [2, 20, 25] 28, [2, 16, 7] 29, [2, 11, 22] 30, [2, 7, 13] 60, [33, 43]	118, [17, 17] 288, [7, 7] 2022, [1, 1]

Voir Bases / Brésiliens

Valeur en base 10 de 2023 en base b Exemple: 20233 => 2×3^3+0×3^2+2×3^1+3×3^0= 6310
2, 23 3, 63 4, 139 5, 263	6, 447 7, 703 8, 1043 9, 1479	10, 2023 11, 2687 12, 3483 13, 4423	14, 5519 15, 6783 16, 8227

Haut de page (ou double-clic)

Retour	Nombre 2022 Nombre 2021 Nombre 2020
Suite	Vœux et humour Noël 2022 – Nouvel an 2023 Jeu avec chiffres de 2023 Nombres de 2024 à 2099 Nombres de 2100 à 2299
Sites	Numbers Aplenty 2023 Année 2023 – Wikipédia 23 and 2023 in Numbers and Pattern – Inder J. Taneja 2020 In Numbers: Mathematical Style – Inder J. Taneja – Très complet sur les façons de faire 2020 en opérations de toutes sortes Numbers Magic – Inder. J. Taneja – Nombreux motifs avec les nombres des années et leurs chiffres
Cette page	http://villemin.gerard.free.fr/NombDico/N1000/N2023.htm