Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 07/11/2024 M'écrire Brèves de Maths

DicoNombre Débutant Glossaire Types de nombres Nombres géométriques Nom des nombres Écriture des nombres Table des facteurs Nombres et anglais Langues	Dictionnaire des Nombres
	1 / 10 / 50 / 70 / 80 / 90 / 100 / 110 / 120 / 125 / 126 / 127 / 128 / 129 / 130 / 131 / 132 / 133 / 134 / 135 / 136 / 137 / 138 / 139 / 140 / 141	142	143 / 144 / 145 / 146 / 147 / 148 / 149 / 150 / 151 / 152 / 153 / 154 / 155 / 160 / 170 / 180 / 190 / 200 / 250 / 300 / 400 / 500 / 1000 / Autres

Cent-quarante-deux

One hundred (and) forty-two

Orthographe / Langues

Facteurs
Diviseurs	1, 2, 71, 142
Binaire	1000 1110
Romain	CXLII

Suite en propriétés arithmétiques

Pair

Composé

Déficient

Somme diviseurs = cube

Non-totient

Congruent

Semi-premier

Géométrique

25 – gonal

Multimédia

142 h/an utilisation du téléphone aux E.-U. en 1997 (60 en Europe).

>>>

Chiffres et numération

142 + 241 = 383 142 – 241 = –99

Devient palindrome en lui ajoutant son retourné et repdigit en lui retirant.

Addition et soustraction

142 = 34 + 35 + 36 + 37 = 4 x 35 + 2

Seule somme de nombres consécutifs >>> Exemple de calcul mental.

Multiplication, division, diviseurs

La somme des diviseurs est un cube.

Avec les puissances

142 = 5² + 6² + 9²	Somme de carrés
142 = 1^3 + 2^3 + 2^3 + 5^3	Somme de cubes.
142 = 2^3 + 3^2 + 5^3 = 2^7 + 3^2 + 5^1	Motif deux fois 2^a + 3^b + 5^c.

En puissance

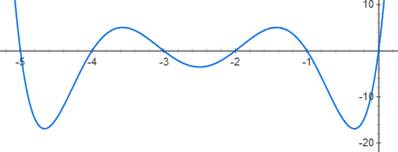
142² = 3 (3+1) (3+2) (3+3) (3+4) (3+5) + 4 Graphe de la courbe x (x+1) (x+2) (x+3) (x+4) (x+5) = x^6 + 15x^5 + 85x^4 + 225x^3 + 274x^2+ 120x

x = 3 et y = 142 Seule solution (hors (0, 0) de l'équation diophantienne: y² – 4 = x(x+1)(x+2)(x+3)(x+4)(x+5) Pour y² – 9 => (1, 27) Pour y² – 25 => (21, 12 875) L.E. Mattics cité par De Koninck

Dénombrement, jeux et curiosités

Jeu du quatre 4.

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération: base, [chiffres]			Repdigit (Brésilien)
142 2, [1, 0, 0, 0, 1, 1, 1, 0] 3, [1, 2, 0, 2, 1] 4, [2, 0, 3, 2] 5, [1, 0, 3, 2] 6, [3, 5, 4] 7, [2, 6, 2] 8, [2, 1, 6] 9, [1, 6, 7] 10, [1, 4, 2] 11, [1, 1, 10]	12, [11, 10] 13, [10, 12] 14, [10, 2] 15, [9, 7] 16, [8, 14] 17, [8, 6] 18, [7, 16] 19, [7, 9] 20, [7, 2] 21, [6, 16]	22, [6, 10] 23, [6, 4] 24, [5, 22] 25, [5, 17] 26, [5, 12] 27, [5, 7] 28, [5, 2] 29, [4, 26] 30, [4, 22] 60, [2, 22]	70, [2, 2] 141, [1, 1]

Voir Bases / Brésiliens

Suite	Nombre 143 Autres nombres
Voir	Nombres par leur nom Empreinte des nombres DicoNombre Junior Historique de ce site et Références Maitres en nombres
Cette page	http://villemin.gerard.free.fr/NombDico/N100a500/Nb143.htm