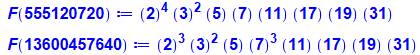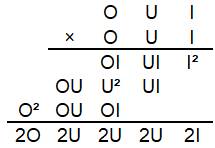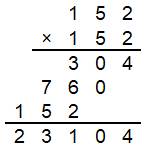Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 28/03/2024 M'écrire Brèves de Maths

DicoNombre Débutant Glossaire Types de nombres Nombres géométriques Nom des nombres Écriture des nombres Table des facteurs Nombres et anglais Langues	Dictionnaire des Nombres
	1 / 10 / 50 / 70 / 80 / 90 / 100 / 110 / 120 / 130 / 135 / 140 / 141 / 142 / 143 / 144 / 145 / 146 / 147 / 148 / 149 / 150 / 151	152	153 / 154 / 155 / 156 / 157 / 158 / 159 / 160 / 161 / 162 / 163 / 164 / 165 / 170 / 180 / 190 / 200 / 250 / 300 / 400 / 500 / 1000 / Autres

Cent-cinquante-deux

One hundred (and) fifty-two

Orthographe / Langues

Facteurs
Binaire	1001 1000
Romain	CLII

Suite en propriétés arithmétiques

Composé

Congruent

Déficient

Docile (amenable)

Dihédral

Gilda

Harshad

Non-totient

Pair

Refactorisable ou tau

Chiffres et numération

152 – (1 + 5 + 2) = 144 = 12²		Devient carré en lui retirant la somme de ses chiffres.
152 = 19 (1 + 5 + 2)		Nombre de Harshad.
15 + 2 = 17 1 + 52 = 53	Formation de nombres premiers en insérant un signe plus entre les chiffres.

Addition et soustraction

152 = 2 + 3 + … + 17	Seule somme de nombres consécutifs >>>
152 = 73 + 79 = 31 + 37 + 41 + 43	Somme de nombres premiers consécutifs.
152 + 304 + 456 215 + 430 + 654	Somme a + 2a + 3a qui présentent six chiffres différents. Impossible d'obtenir neuf chiffres différents avec des termes à trois chiffres. Deux motifs avec permutation des chiffres.

Multiplication, division, diviseurs

152 x 153 x 154 x 155 = 555 120 720 340 x 341 x 342 x 343 = 13 600 457 640		Produit des quatre nombres partageant le même jeu de facteurs.
	Mêmes chiffres pour n et la quantité de facteurs au cube.

Avec les puissances

152 = 2² + 2² + 12² = 4² + 6² + 10² = 4² + 6² + 6² + 8²	Sommes de carrés >>>
152 = 3^3 + 5^3 = (- 4)^3 + 6^3 = 2^3 + 2^3 + 2^3 + 4^3 + 4^3	Nombre binomial. Somme de cubes. Deuxième cas de deux fois somme de deux cubes avec nombres négatifs autorisés; précédent: 91.
152 = 6^3 – 4^3	Nombre binomial.

En puissance

152² = 23 104 & 23 + 04 = 27 = 3^3 251² = 63 001 & 63 + 01 = 64 = 4^3 237² = 56 169 & 56 +69 = 125 = 5^3		Nombres dont la somme des deux chiffres extrêmes du carré est un cube. Les trois seuls carrés à cinq chiffres.
152² = 23 104 = 2^6 x 19^2 179² = 32 041 = 179^2	Carrés formés avec cinq chiffres consécutifs. Deux seuls et avec les mêmes chiffres.
152² = 2 x 11 552 = 23 104	Seul cas en: Résolution pour k = 2 On pose la multiplication du calcul du carré. Attention, les retenues ne sont pas prises en compte. On sait que le résultat en bas est égal à 2 x OOUUI. Si I² = 2I, en termes d'unités, alors I = 2. Si 2UI = 4U = 2U en termes d'unités, et sans retenue (car 2I = 4), alors U = 5. Avec O² comptant pour un seul chiffre, alors O = 1 ou 2. La colonne précédente avec OU + OU et U qui vaut 5, il y a nécessairement une retenue; alors O = 1. Voir Multiplications avec lettres

Dénombrement, jeux et curiosités

Jeu du quatre 4.

Géométrie

152 Types de quartiques planes non réductibles. Courbe d'équation générale p(x,y) = 0 où p est un polynôme irréductible de degré 4 en x et y.

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération: base, [chiffres]			Repdigit (Brésilien)
152 2, [1, 0, 0, 1, 1, 0, 0, 0] 3, [1, 2, 1, 2, 2] 4, [2, 1, 2, 0] 5, [1, 1, 0, 2] 6, [4, 1, 2] 7, [3, 0, 5] 8, [2, 3, 0] 9, [1, 7, 8] 10, [1, 5, 2] 11, [1, 2, 9]	12, [1, 0, 8] 13, [11, 9] 14, [10, 12] 15, [10, 2] 16, [9, 8] 17, [8, 16] 18, [8, 8] 19, [8, 0] 20, [7, 12] 21, [7, 5]	22, [6, 20] 23, [6, 14] 24, [6, 8] 25, [6, 2] 26, [5, 22] 27, [5, 17] 28, [5, 12] 29, [5, 7] 30, [5, 2] 60, [2, 32]	18, [8, 8] 37, [4, 4] 75, [2, 2] 151, [1, 1]

Voir Bases / Brésiliens

Suite	Nombres 155 à 159 Voir haut de page
Voir	Nombres par leur nom Empreinte des nombres DicoNombre Junior Historique de ce site et Références Maitres en nombres
Cette page	http://villemin.gerard.free.fr/NombDico/N100a500/Nb152.htm