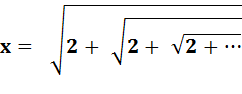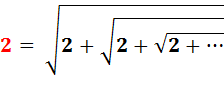|
|||||||||||||||||||||||||||||||||||||
![]()
|
ÉQUATIONS du 2e degré Recherche de nombres Comment
faire usage des équations du deuxième degré pour retrouver des nombres? |
|
|
||
|
Problème Deux
nombres consécutifs, la somme de leur carré est 85. Trouvez ces nombres. Solution |
||
|
|
x et x + 1 |
|
|
|
x² + (x + 1)² = 85 x² + x² + 2x + 1 = 85 2x² + 2x – 84 = 0 x² + x – 42 = 0 |
|
|
b² – 4ac = 1² – 4 . 1
. ( –42) = 1 + 168 = 169 = 13² |
||
|
x1 = – 1/2 – 13/2 = –7 x2 = – 1/2 + 13/2 = 6 |
||
|
|
6 et 7 En effet: 6² + 7² = 36 + 49 = 85 |
|
|
|
x² + x – 42 = 0 x² + 7x – 6x – 42 = 0 x(x + 7) – 6(x + 7) = 0 (x – 6) (x + 7) = 0 x1 = 6 x2 =
–7 |
|
Seules
des solutions positives sont recevables. En
passant de x à son carré, nous nous sommes exposés à cette apparition de
valeurs négatives. |
|
|
||
|
Problème Quel
est le nombre qui ajouté à son inverse donne une somme de 26/5 ? Solution |
||
|
|
x et 1/x |
|
|
|
x + 1/x = 26/5 x² + 1 = 26x / 5 5x² + 5 = 26x 5x² – 26 x + 5 =
0 |
|
|
|
b² – 4ac = 26² – 4.5.5 = 676 – 100 = 576 = 24² |
|
|
|
x1 = (26 – 24) / (2.5) = 2/ 10 = 1/5 x2 = (26 + 24) / (2.5) = 50 / 10 = 5 |
|
|
|
5 En effet: 5 + 1/5 = 26/5 |
|
|
|
5x² – 26 x + 5 =
0 5x² – 25 x – x + 5 = 0 5x(x – 5) – (x – 5) = 0 (5x – 1) (x – 5) = 0 x1 =
1 x2 =
1/5 |
|
La
solution par factorisation est très élégante. Certes ! Mais,
elle est possible que si on connaît pratiquement déjà la solution par avance! |
|
|
||
|
Problème Coupez
100 en deux parts telles que la somme des carrés des parts donne 6 250. Solution |
||
|
|
x et (100 – x) |
|
|
|
x² + (100 – x)² = 6 250 x² + 10 000 – 200x + x² = 6 250 2x² – 200x + 3 750 = 0 |
|
|
|
b² – 4ac = 200² – 4. 2 . 3 750 = 40 000 – 30 000 = 10 000 = 100² |
|
|
|
x1 = (200 – 100) / (2.2) = 100/4 = 25 x2 = (200 + 100) / (2.2) = 300/4 = 75 |
|
|
|
25 et 75 En effet: 25 + 75 = 100 et 25² + 75² = 625 + 5 625 = 6 250 |
|
|
|
2x² – 200x + 3
750 = 0 2x² – 150x – 25x + 3 750 = 0 2x(x – 25) – 150(x – 25) = 0 (2x – 150) (x – 25) = 0 x1 =
150/2 = 75 x2 =
25 |
|
|
||
|
Problème Deux
nombres, leur somme vaut 20 et leur produit 91. Trouvez
ce nombre. Solution |
||
|
|
x et (20 – x) |
|
|
|
x (20 – x) = 91 20x – x² = 91 x² – 20x + 91 = 0 |
|
|
|
b² – 4ac = 20² – 4 . 91 = 400 – 364 = 36 = 6² |
|
|
|
x1 = (20 – 6) / 2 = 7 x2 = (20 + 6) / 2 = 13 |
|
|
|
7 et 13 En effet: |
|
|
|
x² – 20x + 91 =
0 x² – 7x – 13x + 91 = 0 x(x – 7) – 13(x – 7) = 0 (x –13) (x – 7) = 0 x1 =
13 x2 =
7 |
Voir Somme et produit
|
|
||
|
Problème Un
nombre ajouté à son carré donne une somme de 42. Trouvez
ce nombre. Solution |
||
|
|
x |
|
|
|
x + x² = 42 x² + x – 42 = 0 |
|
|
|
b² – 4ac = 1² – 4 . (–42) = 1 + 168 = 169 = 13² |
|
|
|
x1 = (–1 – 13) / 2 = –7 x2 = (–1
+ 13) / 2 = 6 |
|
|
|
6 Seule la racine positive est admissible En effet: 6 + 6² = 6 + 36 = 42 |
|
|
|
x² + x – 42 = 0 x² + 7x – 6x – 42 = 0 x(x + 7) – 6(x + 7) = 0 (x – 6) (x + 7) = 0 x1 =
6 x2 =
–7 |
|
|
||
|
Problème Un
nombre à 2 chiffres. Le produit des chiffres est 14. En
ajoutant 45 au nombre les chiffres sont inversés. Trouvez
ce nombre. Solution |
||
|
|
x et y N = 10x + y |
|
|
|
10x + y + 45 = 10y + x 9x – 9y = – 45 x – y = –5 x = y – 5 |
|
|
|
x . y = 14 (y – 5) y = 14 y² – 5y – 14 = 0 |
|
|
|
b² – 4ac = 25 – 4 . 1
. (–14) = 25 + 56 = 81 = 9² |
|
|
|
y1 = (5 – 9) / 2 = – 2 y2 = (5 + 9) / 2 = 7 |
|
|
|
y = 7 Seule la racine positive est admissible x = 7 – 2 = 2 N = 27 En effet: 27+ 45 = 72 |
|
|
|
y² – 5y – 14 = 0 y² – 7y + 2y – 14 = 0 y(y – 7) + 2(y – 7) =
0 (y + 2) (y – 7) = 0 x1 =
–2 x2 =
7 |
|
|
||
|
Problème
Trouvez
ce nombre. Solution |
||
|
|
|
|
|
|
x² = 2 + x x² – x – 2 = 0 |
|
|
|
b² – 4ac = 1² – 4 . 1
. (–2) = 1 + 8 = 9 = 3² |
|
|
|
x1 = (1 + 3) / 2 = 2 x2 = (1
– 3) / 2 = –1 |
|
|
|
|
|
Voir Deux / Racines
continues
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()