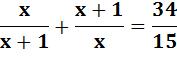|
|||||||||||||||||||||||||||||||||||||
![]()
|
ÉQUATIONS du 2e degré Cas simples et cas particuliers Pour
s'initier au cas général. Ou reconnaître les cas faciles.
|
|
|
|||
|
Cas où a = 1
Voir Somme et produit Réciproquement Si a = 1
et b = – (c+1), alors les racines sont 1 et c. |
x² +
b x + c = 0 Racines 1 et c et alors b = – (c+1) |
x² –
3x + 2 = 0 Racines x = 1 et x = 2 Factorisation (x - 1) (x - 2) = 0 |
|
|
|
En effet: 1² + b .1 + c = 0 1 + b + c = 0 |
|
|
|
Cas général (a Si a + b + c = 0, l'une des racines
est 1 Et l'autre vaut c/a. |
a + b + c = 0 Racines 1 et c/a |
2x² – 8x + 6 = 0 2 – 8 + 6 = 0 alors x = 1 et x = 6/2 = 3 |
|
Si a - b + c = 0, l'une des racines est – 1 Et l'autre vaut -c/a. |
a - b +c = 0 Racines –1 et –c/a |
2x² + 8x + 6 = 0 2 – 8 + 6 = 0 alors x = – 1 et x = -6/2 = – 3 |
Voir Racine unité pour b et c de -10 à +10
|
|
||
|
Cas particulier Si
le côté gauche, ax² + bx + c peut
être factorisé sous la forme: a(x – u)
(x – v) Alors, u et v sont les solutions
(racines) de l'équation. |
Exemple x² + x – 2 = 0 x² – x + 2x – 2 = 0 x (x – 1) + 2(x – 1) = 0 (x – 1) (x + 2) = 0 Racines u = 1 et v = –2 |
|
|
Avec identités
remarquables |
|
||
|
Équations |
Racines |
Exemples |
|
|
x² – b² = 0 (x – b) (x + b) = 0 |
Racines x = b x = –b |
x² – 25 = 0 x = 5 x= –5 |
|
|
x² + 2bx + b² = 0 = (x + b)² = 0 |
Racine double x = –b |
x² + 4x + 4 = 0 x = –2 |
|
|
a²x² + 2abx + b² =
0 = (ax + b)²
= 0 |
Racine double x = –b/a |
4x²+ 40x + 100 = 0 x = –10/2 = = –5 |
|
Voir Identités
|
|
|||
|
Équations |
Explications |
Racines |
|
|
(x – 4) (x – 2) = 0 |
Cas déjà factorisé |
x = 4 et x = 2 |
|
|
(x – 4) (x + 2) = 0 |
|
x = 4 et x = – 2 |
|
|
(2x + 3) ( 5x – 7) = 0 |
|
x = – 3/2 et x = 7/5 |
|
|
x² + 3x – 18 = 0 |
Il faut trouver la factorisation x²
+ 6x – 3x – 18 = x(x + 6) – 3(x + 6) = (x – 3) (x + 6) |
x = 3 et x = – 6 |
|
|
6x² – x – 2 = 0 |
6x² – 4x + 3x – 2 = 2x (3x – 2) + (3x –2) = (2x + 1) (3x – 2) |
x= – 1/2 et x = 2/3 |
|
|
2x² + ax – a² = 0 |
2x² + ax
– a² = 2x² + 2ax – ax – a² = 2x (x + a) – a (x + a) = (2x – a) (x + a) |
x = a/2 et x = – a |
|
|
|
x
/ (x+1) + (x+1) / x = x² / (x² + x) + (x+1)² / (x² + x) = (x² + x² + 2x + 1) / (x² + x) = (2x² + 2x + 1) / (x² + x) En reprenant l'équation (2x² + 2x + 1) / (x² + x) = 34/15 Le produit en croix 15 (2x² + 2x + 1) = 34 (x² + x) 30x² + 30x + 15 = 34x² + 34x 4x²
+ 4x – 15 = 0 Factorisation
4x² + 4x – 15 =
4x² + 10x – 6x – 15 = 2x (2x + 5) – 3 (2x + 5) = (2x – 3) (2x + 5) |
x = 3/2 et x = –5/2 |
|
|
EXERCICES à
"tiroir" |
|
||
|
Équations |
Explications |
Racines |
|
|
(x–3)/(x+3) –
(x+3)/(x–3) = 48/7 |
Posons y = (x–3)/(x+3) Alors (x+3)/(x–3) = 1/y et l'équation devient y –
1/y = 48/7 |
|
|
|
y – 1/y = 48/7 |
(y² – 1) / y =
48/7 7 (y² – 1) =
48y 7y² – 48y – 7 =
0 7y² – 49y + y –
7 = 0 7y(y – 7) +
(y–7) = 0 (7y+1)
(y–7) = 0 |
y = –1/7
et y = 7 |
|
|
y = (x–3)/(x+3) = –1/7 |
7x – 21 = –x – 3 8x = 18 x = 18/8 = 9/4 |
x1 = 9/4 |
|
|
y = (x–3)/(x+3) = 7 |
x – 3 = 7x + 21 6x = –24 x = –4 |
x2 = –4 |
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()