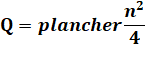NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 20/10/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	ADDITION
Débutants Addition	PARTITIONS						Glossaire Addition
INDEX Partition Calculs	Approche			En bref et Index		S'y retrouver
	Formules de récurrence			Quantité de partitions		Partielles (1/2) – (2 / 2)
	Fonction génératrice			P(1) à P(6)	P(7) à P15)	K-Bonacci
	Digi-P	Diff-P		Bi-P	Tri-P	Pri-Bi-P		Pri-Tri-P
			Sommaire de cette page >>> Bipartition >>> Somme de deux nombres >>> Quantité de bi-compositions >>> Bipartition et produit maximum

BIPARTITIONS

Deux cas:

Partition d'un nombre avec deux nombres (sommants).

Bipartition sous contrainte: avec les seuls deux nombres 1 et 2.

BIPARTITION – 2 Sommants

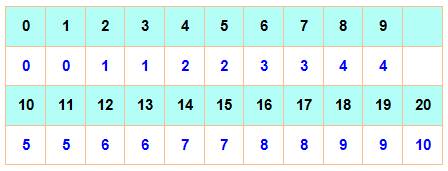
Bipartition des nombres de 1 à 10

n	a1	a2	qté
2	1	1	1
3	1	2	1
4	1	3	2
	2	2
5	1	4	2
	2	3
6	1	5	3
	2	4
	3	3
7	1	6	3
	2	5
	3	4
8	1	7	4
	2	6
	3	5
	4	4
9	1	8	4
	2	7
	3	6
	4	5
10	1	9	5
	2	8
	3	7
	4	6
	5	5

Quantité de bipartitions

n	qté
1	0
2	1
3	1
4	2
5	2
6	3
7	3
8	4
9	4
10	5
11	5
12	6
13	6
14	7
15	7
16	8
17	8
18	9
19	9
20	10
21	10
22	11
23	11
24	12
25	12

Somme de deux nombres (bipartition)
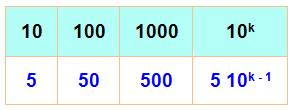
Combien de sommes de deux nombres pour faire 10 ? 5 possibilités Combien de sommes de deux nombres pour faire 100? 50 possibilités
Ensuite …
Évolution: incrémentation de 1 à chaque nombre pair.

Bi-Composition – Les 2 nombres 1 et 2
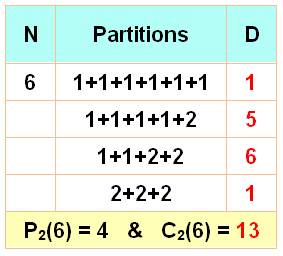
Bi-Composition et Fibonacci Avec l'exemple du nombre 6, on compte 4 partitions avec les seuls nombres 1 et 2. En comptant toutes les permutations, on compte 13 compositions du nombre 6 avec les seuls nombres 1 et 2. On a montré que: C2(n) = F2n Fibonacci: 1, 1, 2, 3, 5, 8, 13, … (le 6^e en commençant par F0 = 1).
Polynôme générateur de la suite de Fibonacci Le polynôme visualisé en première ligne bleue. Il s'agit de la division de l'unité par le polynôme (1 – z – z²). Les coefficients de son développement en série sont les nombres de Fibonacci (deuxième ligne bleue). Identités valables pour z compris entre 0 et 1. Il suffit de les extraire avec l'instruction coefficients et, les uns après les autres, par l'instruction séquence.	Bipartition (1, 2) – Traitement avec le logiciel Maple

Voir Formule de récurrence

Bipartition et produit maximum
Bipartition maximale		Pour chaque nombre n, on cherche la bipartition qui donne le produit le plus grand
Propriété		Exemples avec n = 5, on a 3 x 2 = 6 (écart 1) avec n = 6, on a 3 x 3 = 9 (écart 0) Si n est pair, les deux nombres de la bipartition sont n/2 et le produit est un carré. Si n est impair en 2k + 1, les deux nombres sont k et k + 1. Formule Voir Arrondi, plancher et plafond		n, a, b, Produit, Écart
Suite pour n de 1 à 100		0, 1, 2, 4, 6, 9, 12, 16, 20, 25, 30, 36, 42, 49, 56, 64, 72, 81, 90, 100, 110, 121, 132, 144, 156, 169, 182, 196, 210, 225, 240, 256, 272, 289, 306, 324, 342, 361, 380, 400, 420, 441, 462, 484, 506, 529, 552, 576, 600, 625, 650, 676, 702, 729, 756, 784, 812, 841, 870, 900, 930, 961, 992, 1024, 1056, 1089, 1122, 1156, 1190, 1225, 1260, 1296, 1332, 1369, 1406, 1444, 1482, 1521, 1560, 1600, 1640, 1681, 1722, 1764, 1806, 1849, 1892, 1936, 1980, 2025, 2070, 2116, 2162, 2209, 2256, 2304, 2352, 2401, 2450, 2500, … OEIS A002620
Suite indexée [n, Q)] pour n de 1 à 100		[1, 0], [2, 1], [3, 2], [4, 4], [5, 6], [6, 9], [7, 12], [8, 16], [9, 20], [10, 25], [11, 30], [12, 36], [13, 42], [14, 49], [15, 56], [16, 64], [17, 72], [18, 81], [19, 90], [20, 100], [21, 110], [22, 121], [23, 132], [24, 144], [25, 156], [26, 169], [27, 182], [28, 196], [29, 210], [30, 225], [31, 240], [32, 256], [33, 272], [34, 289], [35, 306], [36, 324], [37, 342], [38, 361], [39, 380], [40, 400], [41, 420], [42, 441], [43, 462], [44, 484], [45, 506], [46, 529], [47, 552], [48, 576], [49, 600], [50, 625], [51, 650], [52, 676], [53, 702], [54, 729], [55, 756], [56, 784], [57, 812], [58, 841], [59, 870], [60, 900], [61, 930], [62, 961], [63, 992], [64, 1024], [65, 1056], [66, 1089], [67, 1122], [68, 1156], [69, 1190], [70, 1225], [71, 1260], [72, 1296], [73, 1332], [74, 1369], [75, 1406], [76, 1444], [77, 1482], [78, 1521], [79, 1560], [80, 1600], [81, 1640], [82, 1681], [83, 1722], [84, 1764], [85, 1806], [86, 1849], [87, 1892], [88, 1936], [89, 1980], [90, 2025], [91, 2070], [92, 2116], [93, 2162], [94, 2209], [95, 2256], [96, 2304], [97, 2352], [98, 2401], [99, 2450], [100, 2500]
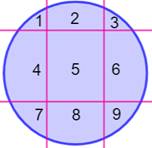
Application	Quantité maximale de parts de pizza produites par n = c + 2 coupes successivement parallèles et perpendiculaires. Exemple avec 4 coupes, n = 6 et la table donne 9, comme le montre aussi la figure. Voir Nombres pizzas
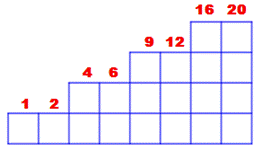
	Quantité de blocs au rang n dans un escalier progressant par double-marche.

Voir Brève 767

Retour	Partition stricte (avec nombres différents) Partition sous contraintes
Suite	Bipartitions avec des nombres premiers Tripartitions Partitions – Index
Voir	Addition - Glossaire Addition des carrés Addition des entiers Addition des puissances Carrés magiques Conjecture de Goldbach Multi-somme de puissances S'y retrouver Totient d'Euler
Site	OEIS A002620 – Quarter-squares: floor(n/2)*ceiling(n/2).
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Addition/PttBi.htm