|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
PRIM-TRIPARTITION Nombre égal à la somme de trois nombres premiers. Vers la conjecture de Goldbach. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Exemples
de primtripartition
Quantité de primtripartition
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Conjecture
de Goldbach forte En 1742, Goldbach écrit à Euler: Tout nombre supérieur
à 5 est la somme de trois nombres premiers: Nsup5 = P + P + P. |
|
Voir développement en Conjecture de
Goldbach / Nombres premiers
|
|
|
|
3 3 89 3 13 79 3 19 73 3 31 61 5 7 83 5 11 79 5 17 73 5 19 71 5 23 67 5 29 61 5 31 59 5 37 53 5 43 47 7 17 71 7 29 59 7 41 47 11 11 73 11 13 71 11 17 67 11 23 61 11 31 53 11 37 47 11 41 43 13 23 59 13 29 53 13 41 41 17 17 61 17 19 59 17 31 47 17 37 41 19 23 53 19 29 47 23 29 43 23 31 41 29 29 37 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Classons
selon le nombre de primtripartitions
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
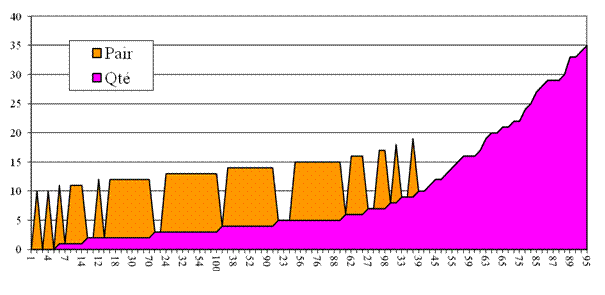
Illustration
de 1 à 100
|
|
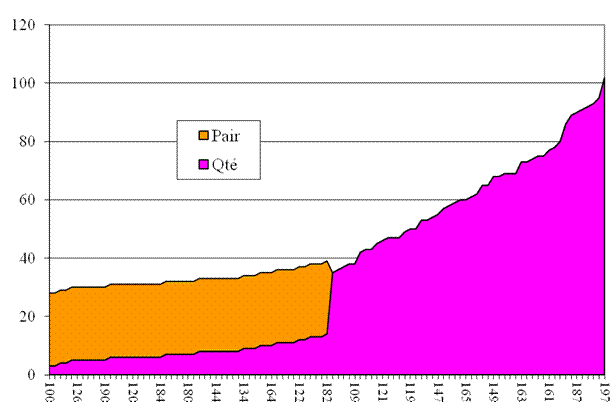
de
100 à 200
182 donne 14 primtripartitions. 105 donne 35 primtripartitions. |
|
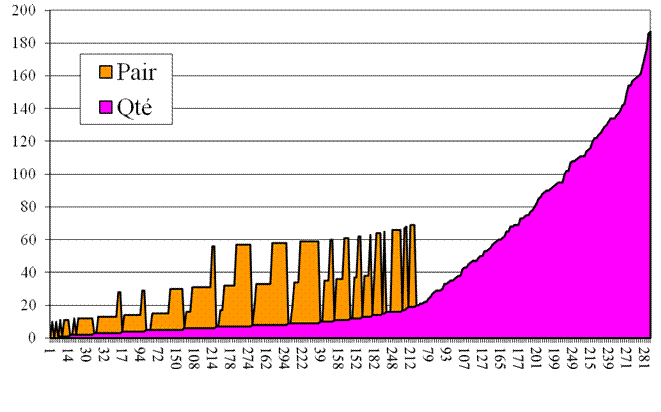
De
1 à 300 Rappel Abscisse: les nombres ordonnés par quantité
croissante de partitions. Qté = quantité de
décompositions en sommes de trois nombres premiers; la valeur est se lit sur l'échelle des
ordonnées. Pair = codage en orange des nombres pairs.
|
![]()
|
Retour |
|
|
Suite |
|
|
fVoir |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Addition/PttPrTri.htm
|
![]()