NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 26/01/2018 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	ADDITION
Débutants Addition	PARTITIONS						Glossaire Addition
INDEX Partition Calculs	Approche			En bref et Index		S'y retrouver
	Formules de récurrence			Quantité de partitions		Contraintes (1/2) – (2 / 2)
	Fonction génératrice					K-Bonacci
	Digi-P	Diff-P		Bi-P	Tri-P	Pri-Bi-P		Pri-Tri-P
			Sommaire de cette page >>> Bipartition en nombres premiers >>> Primbipartitions & pairs / impairs >>> Conjecture de Goldbach >>> Zoom

PRIM-BIPARTITION

Nombre égal à la somme de deux nombres premiers.

Vers la conjecture de Goldbach.

BIPARTITION en NOMBRES PREMIERS

Prim-bipartition des nombres de 0 à 20

n	a1	a2	qté
0			0
1			0
2			0
3			0
4	2	2	1
5	2	3	1
6	3	3	1
7	2	5	1
8	3	5	1
9	2	7	1
10	3	7	2
	5	5
11			0
12	5	7	1
13	2	11	1
14	3	11	2
	7	7
15	2	13	1
16	3	13	2
	5	11
17			0
18	5	13	2
	7	11
19	2	17	1
20	3	17	2
	7	13

Certains nombres ne sont pas la somme de deux premiers.
Comme 11 et 17.

Ils sont tous les deux impairs.

PRIM-BIPARTITIONS & PAIRS / IMPAIRS

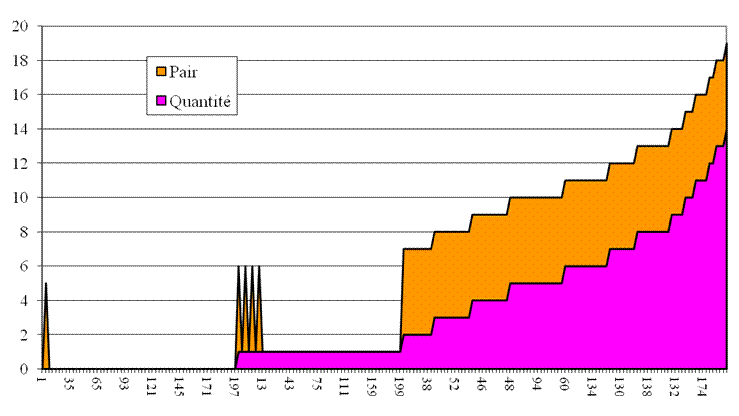
Primbipartition et pairs / impairs On classe les nombres selon la quantité croissante de bipartitions en nombres premiers. On fait ressortir les nombres pairs en les marquant en orange (hauteur mise arbitrairement à 5 sur le graphique pour offrir une bonne visibilité). Avec les nombres de 1 à 200 À gauche les impairs et à droite les pairs: Note Les valeurs en abscisse correspondent aux nombres de 1 à 200 classés par valeur croissante de leur quantité de primbipartitions. Elles ne sont pas toutes visibles. Le premier pic orange correspond au chiffre "2". Pour les quatre pics suivants, voir zoom Lecture du graphique Tous les nombres pairs (sauf le "2") sont superposés sur la courbe mauve: Ils sont tous décomposables en somme de deux nombres premiers, au moins une fois (partie droite du graphique: orange tout le temps sur le mauve) Les nombres impairs sont, ou non, décomposables en sommes de deux nombres premiers Mais, dans le cas où ils sont décomposables, ils le sont en faible quantité de possibilités (Ils sont tous dans la partie gauche du graphique)

CONJECTURE DE GOLDBACH
Conjecture de Goldbach forte Tout nombre pair positif est la somme de 2 nombres premiers: E = P + P. E: pour nombre pair (Even en anglais)

Voir développement en Conjecture de Goldbach

ZOOM

Parmi les nombre de 0 à 200, voici

les plus grands nombres non décomposables (197)

les quatre nombres pairs décomposables une seule fois.

187	0
189	0
191	0
197	0
4	1	Pair
5	1
6	1	Pair
7	1
8	1	Pair
9	1
12	1	Pair
13	1
15	1

Ceci est un extrait du tableau qui a servi à construire la courbe ci-dessus.
Zoom sur la partie comportant les quatre pics orange.

Note orange (couleur) est invariable.

Retour	Tripartition Partition sous contraintes
Suite	Bipartitions avec des nombres premiers Bipartition avec des premiers Partitions – Index
Voir	Addition - Glossaire Addition des carrés Addition des entiers Addition des puissances Carrés magiques Conjecture de Goldbach Multi-somme de puissances S'y retrouver Totient d'Euler
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Addition/PttPrBi.htm