NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 01/12/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Carrés magiques
Débutants Carrés magiques	Carré magique 5 x 5				Glossaire Carrés magiques
INDEX Carrés magiques Ordres Constructions Magie Jeux de grilles Jeux et énigmes	Carré 5 x 5	Construction	Diaboliques	Générique
	Propriétés	Premiers	Pheru	Gigogne
	Const. Symétries
		Sommaire de cette page >>> Carré magique 5 x 5 >>> Carré diabolique d'ordre 5 >>> Curiosités >>> Calcul des sommes

Carré MAGIQUE d'ordre 5

Intéressant, car nombreux et vite diaboliques

Voir Mon premier carré magique d'ordre 5

Carré magique 5 x 5

Ce carré magique utilise tous les nombres de 1 à 25.
La somme magique est ½ n (n² + 1) = ½ 5 x 26 = 65.
Ce carré est simplement magique: les diagonales secondaires ne donnent pas toutes la somme magique.

C'est le carré d'ordre 5 le plus connu et sans doute le plus ancien

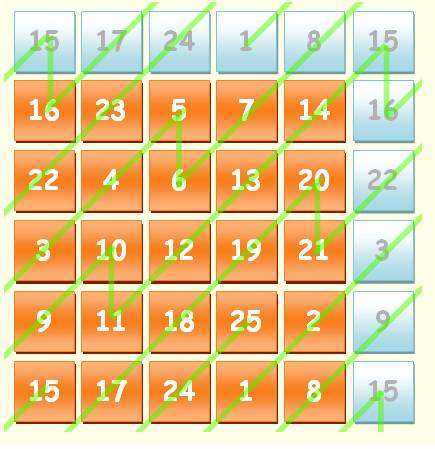
Construction

Observez la diagonale en bleu: tous les nombres de 11 à 15: toutes les pandiagonales sont de même facture à condition d'imaginer que le carré s'enroule sur lui-même.

Chaque fois qu'un multiple de 5 est atteint, alors le nombre suivant est placé en dessous.

Le deuxième carré est construit de la même manière avec le 1 du départ placé ailleurs.

	17	24	1	8	15	65
	23	5	7	14	16	65
	4	6	13	20	22	65
	10	12	19	21	3	65
	11	18	25	2	9	65
65	65	65	65	65	65	65

Carré magique et associatif: la somme de deux nombres opposés équidistants du centre est constante: 17 + 9 = 24 + 2 = 5 + 21 = … = 2 x 13 (le nombre central)

	16	23	5	7	14	65
	22	4	6	13	20	65
	3	10	12	19	21	65
	9	11	18	25	2	65
	15	17	24	1	8	65
65	65	65	65	65	65	65

Carré magique semblable au précédent, mais il n'est plus associatif.

L'harmonie du carré magique d'ordre 5

Ce dessin illustre une des méthodes de construction des carrés magiques dite siamoise ou de Loubère (un Français qui est allé au Siam, ancien nom de la Thaïlande).

Cette méthode consiste à progresser régulièrement d'un certain vecteur ici: (1,1) et à décrocher d'un autre vecteur ici: (0,-1) lorsqu'il n'est plus possible de progresser régulièrement (cas d'un multiple de n). Elle est généralisable en définissant d'autres vecteurs.

Avec les vecteurs (2,1) et (1, -1), on retrouve la méthode classique du cavalier et, avec le 1 sur le milieu d'un bord, le carré est panmagique.

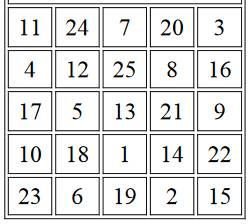
Ce carré magique est construit en respectant le mouvement du cavalier: 2 pas vers le haut et 1 pas vers la droite.

Décrochage d'un pas vers le bas pour tout multiple de 5.

Toutes les diagonales et pandiagonales somment aussi en 65.

Voir Explications détaillées

	10	18	1	14	22	65
	11	24	7	20	3	65
	17	5	13	21	9	65
	23	6	19	2	15	65
	4	12	25	8	16	65
65	65	65	65	65	65	65

Carré magique, associatif et panmagique.

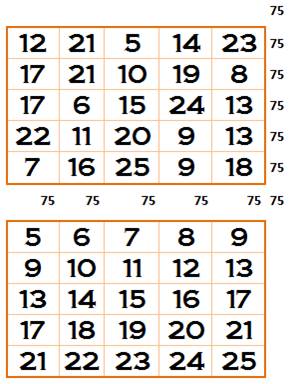
Avec des nombres presque quelconques La suite de nombres indiquée dans le tableau du bas a été placée dans le tableau du haut selon la méthode de construction des carrés magiques dit de De la Loubère. Ça marche, même avec ces séries bizarres de nombres!

Carré magique avec suite de nombre particulière

CARRÉ DIABOLIQUE D'ORDRE 5

Ordre 5

Nombres de 1 à n² = 25

Somme magique
S = n (n² + 1) / 2
= 5 (25+1)/2 = 65

1	15	24	8	17
23	7	16	5	14
20	4	13	22	6
12	21	10	19	3
9	18	2	11	25

Ce carré est MAGIQUE,

Avec 12 fois la somme 65

5 rangées,

5 colonnes

2 diagonales

Il est aussi DIABOLIQUE

Avec 56 fois la somme 65

Sur toutes les pandiagonales:

4 + 4 fois

Sur des "carrés, croix et étoiles":

1+17+9+25+13: 2 fois,

1+15+23+7+19: 4 fois

7+16+4+13+25: 4 fois

23+7+20+4+11: 8 fois

15+23+7+16+4: 9 fois

1+24+7+20+13 : 9 fois

CURIOSITÉS
La somme des deux nombres extrêmes vaut 1 + 25 = 26 La case centrale vaut la moitié: 13. Il est associatif de somme 26. En éliminant la grande couronne, il reste encore associatif de somme 26 (7+19=26). En comptant la case centrale, on trouve 13 fois (26/2) la somme 26.	Ce carré est MAGIQUE, SUPER-ASSOCIATIF et PANDIAGONAL Il est Super-DIABOLIQUE

Calcul des sommes possibles (algébriques)

S = somme algébrique des + et – et, aussi la somme des *

N = nombres de combinaisons.

+

+

+

+

*

+

+

+

+

+

+

+

+

*

+ *

*

+

*

+

S=

65

N=

9

S=

65

N=

9

S=

65

N=

2

+

+

–

–

+

+

+

–

+

+

–

+

+

S=

65

N=

16

S=

0

N=

16

S=

0

N=

12

	–				–
						+	+	+
+	+	+				+	+
+	+	+				+
S=	65		N=	16	S=	65		N=	8

Bonus

Suite	Carré 5 x 5 suite Carré 5 x 5 – Losange Carré 5 x5 – Méthode des symétries Carré d'ordre 6 et plus Carrés magiques – Index
Voir	Carrés – les nombres Carrés en géométrie Carrés mystérieux Dominos magiques Énigmes Géométrie Humour Jeux Jeux de chiffres Nombres consécutifs Nombres en chiffres Nombres magiques - Index Pannumérique Paradoxes Propriétés du carré magique Rubriques débutants Sudoku
Diconombre	Nombre 5 Nombre 25 Nombre 65
Sites	Liens vers les sites carrés magiques
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/CMordre5.htm