NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 01/12/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Carrés magiques
Débutants Carrés magiques	Carré magique 4 x 4			Glossaire Carrés magiques
INDEX Carrés magiques Jeux	Carré 4 x 4	Décompte	Formules	Premiers
	Carré mental	Propriétés Classement	Relations	Pandiagonaux
	Plus que parfait		Cousinage	Franklin
		Sommaire de cette page >>> Revue des propriétés >>> Classement en 12 catégories

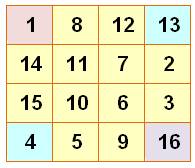
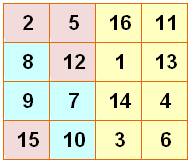
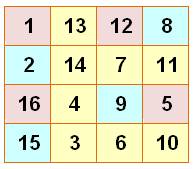
Carré magique 4 x 4

PROPRIÉTÉS & CLASSEMENT

Nous allons

examiner quelques propriétés relatives à tous ou à certains carrés magiques d'ordre 4, et

classer ces carrés en reprenant la classification d'Henry Dudeney (1910) en douze catégories.

Revue synthétique des propriétés du carré 4x4
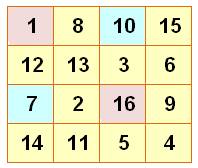
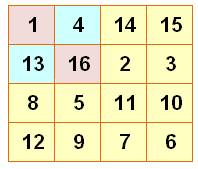
Plus que parfait	Tous les carrés 2x2 produisent la somme magique.		>>>
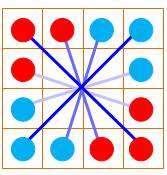
Associatif	La somme des extrémités des six diamètres est égale à la moitié de la somme magique		>>>
Panmagique	En plus des diagonales principales, les six diagonales secondaires (pandiagonales) sont magiques.		>>>
Semi-panmagique	En plus des diagonales principales, deux diagonales secondaires sont magiques.		>>>
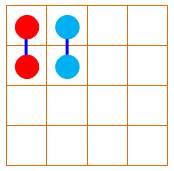
Dominos	Les rectangles 2x1 horizontaux ne produisent que deux sommes, et même chose pour les verticaux		>>>
Somme 3x3	Les sommets des carrés 3x3 produisent la somme magique		>>>
Somme2x2	Recense la quantité de carrés 2x2 magiques. Le carré central de tout carré magique 4x4 donne la somme magique.		>>>
Triangle 3x3	Somme des six nombres dans les triangles rectangles selon les quatre orientations, soit 4 x16 possibilités		>>>
Concaténation	Somme de lignes ou colonnes formées par la juxtaposition des nombres de deux lignes ou deux colonnes		>>>

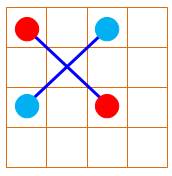
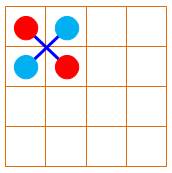
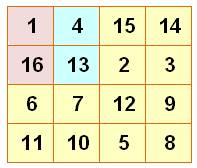
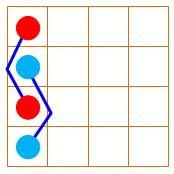
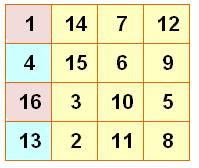
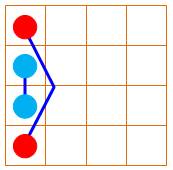
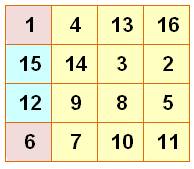
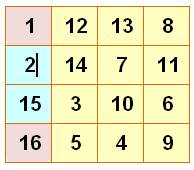
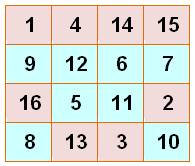
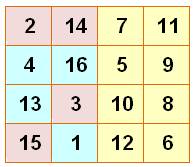
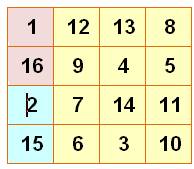
Les 16 nombres du carré magique organisés en 8 paires

Pour tout carré magique d'ordre 4, il possible associer les seize nombres par paires de sorte que le total soit égal à 34, la moitié de la constante magique. Dudeney a classé ces carrés en douze catégories selon la configuration des huit paires.

Classement des Carrés Magiques 4x4 selon les huit paires de nombres
Groupe Qté	Configuration	Description	Exemple	Propriétés
1 48		Quatre fois ce motif. 8 fois les sommets des carrés 3 x 3.		Plus que parfait Panmagique: 6 Dominos: 8H 8V Sommes 3x3: 4 Somme 2x2: 16 Triangle 3x3: 4x16
2 48		Quatre fois ce motif. 8 fois les sommets des carrés 2 x 2.		Semi-panmagique: 2 Diagonale en V: 4 Dominos: 0 Sommes 3x3: 0 Somme 2x2: 8 Triangle 3x3: 0
3 48		Une fois ce motif. 8 fois les extrémités des diagonales.		Associatif Semi-panmagique: 2 Dominos: 8H 8V Sommes 3x3: 0 Somme 2x2: 8 Triangle 3x3: 0, mais régulier avec 4 sommes: 61, 41, 45 et 57
4 96		Quatre fois ce motif. 8 fois les dominos verticaux.		Semi-panmagique: 2 Dominos: 0H 8V Sommes 3x3: 0 Somme 2x2: 12 Triangle 3x3: 0
5 96		Quatre fois ce motif. 8 fois les sommets du rectangle 3 x 1.		Semi-panmagique: 2 Dominos: 8H 0V Sommes 3x3: 4 Somme 2x2: 8 Triangle 3x3: 0
6 96		Quatre fois ce motif. 4fois les sommets extrêmes et 4 fois les sommets centraux sur une colonne.		Semi-panmagique: 2 Dominos: 0H 0V Sommes 3x3: 4 Somme 2x2: 12 Triangle 3x3: 0
6' 208	id.	id.		Pandiagonale: 0 Dominos: 0H 0V Sommes 3x3: 0 Somme 2x2: 8 Triangle 3x3: 0

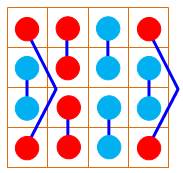
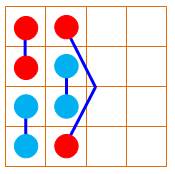
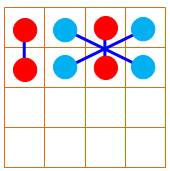
7 56		Une fois ce motif.		Pandiagonale: 0 Dominos: 0H 0V Sommes 3x3: 0 Somme 2x2: 8 Triangle 3x3: 0
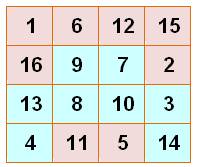
8 56		Deux fois ce motif. avec symétrie verticale.		Pandiagonale: 0 Dominos: 0H 0V Sommes 3x3: 0 Somme 2x2: 4 Triangle 3x3: 0
9 56		Deux fois ce motif. avec symétrie verticale.		Pandiagonale: 0 Dominos: 0H 0V Sommes 3x3: 0 Somme 2x2: 8 Triangle 3x3: 0
10 56		Deux fois ce motif. avec symétrie verticale.		Pandiagonale: 0 Dominos: 0H 0V Sommes 3x3: 0 Somme 2x2: 4 Triangle 3x3: 0
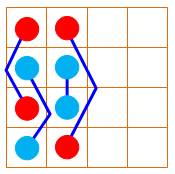
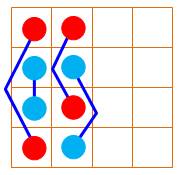
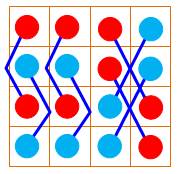
11 8		Deux fois ce motif. avec symétrie horizontale.		Semi-panmagique: 2 Dominos: 0H 0V Sommes 3x3: 0 Somme 2x2: 8 Triangle 3x3: 0
12 8		Une fois ce motif.		Pandiagonale: 0 Dominos: 0H 0V Sommes 3x3: 0 Somme 2x2: 4 Triangle 3x3: 0

Suite	Carré diabolique de Dürer Carré de la Sainte Famille Exemple de calcul sur un carré 4 x 4 Carré 5 x 5 Carrés magiques – Index
Voir	Carrés – les nombres Carrés en géométrie Carrés mystérieux Dominos magiques Géométrie Humour Jeux Jeux de chiffres Nombres consécutifs Nombres magiques - Index Pannumérique Rubriques débutants Sudoku Propriétés du carré magique
Diconombre	Nombre 3 Nombre 12 Nombre 15 Nombre 34
Sites	Liens vers les sites carrés magiques Order 4 Magic Squares – Harvey Heinz – Plus que complet, y compris la liste des 880 carrés magiques.
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/CMor4Cla.htm