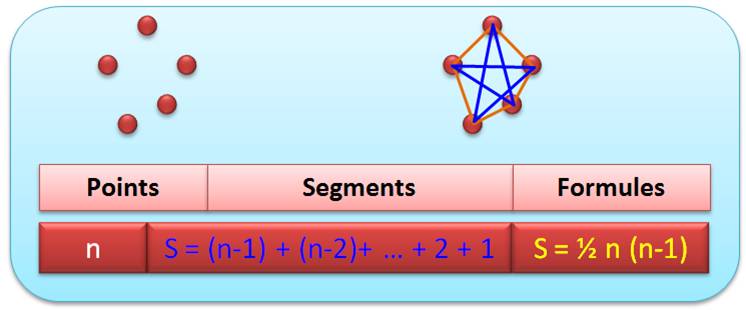
compter les segments dans un polygone

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 28/03/2023 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Dénombrement
Débutants Général	COMPTER des …				Glossaire Général
INDEX Compter Dénombrement	Nombres	Fractions	Ensembles	Droites
	Escalier	Chemins sur grille	Trajets	Régions
		Sommaire de cette page >>> Polygone >>> SEGMENTS – Dénombrement *>>>* SEGMENTS – Total *>>>* SEGMENTS – Formule *>>>* Diagonales >>> Conclusion >>> Cube

COMPTER les SEGMENTS

Compter les diagonales d'un pentagone ou d'un polygone.

Compter les segments dans un cube ou dans un polyèdre.

Etc.

Quantité de segments (s) pour n points ou n sommets

Voir Graphe simple complet

POLYGONE
Exemple du pentagone Partons d'un polygone de n côtés. On note qu'il a aussi n sommets.
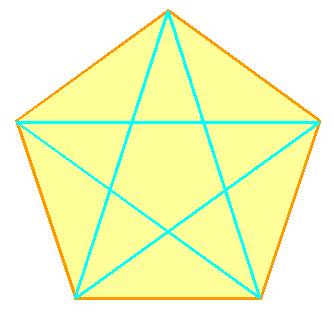
Propriétés Quantité totale de segments (s) *égale* Quantité de côtés (n) *plus* Quantité de diagonales (d) s = n + d	n + d = 5 + 5 = 10 segments

SEGMENTS – Dénombrement

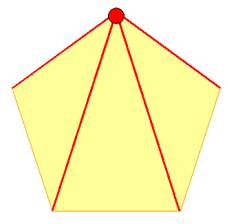
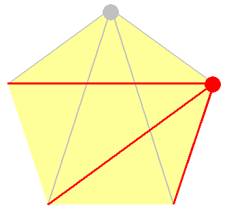
Prenons le premier point: on peut joindre tous les points (n), sauf le point considéré (-1);

soit la formation de n – 1 segments.

n – 1 = 4 segments

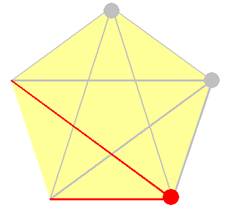
Avec le deuxième point: on peut aussi joindre tous les points (n), sauf le point considéré (-1) et SAUF le premier point déjà vu (-1);

soit la formation de n – 2 segments.

n – 2 = 3 segments

Avec le troisième point: on peut aussi joindre tous les points (n), sauf le point considéré (-1) et SAUF les deux points déjà vu (-2);

soit la formation de n – 3 segments.

n – 3 = 2 segments

On continue avec les autres points:
Le 4^e qui donne n - 4 segments;
Le 5^e qui donne n - 5 segments;

Le (n - 2)^e , ou avant avant-dernier

qui donne n - (n-2) segments.

…

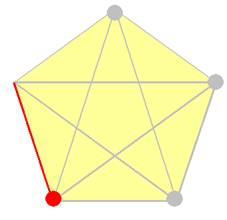
Avec l'avant dernier point, le (n-1)^e : on peut joindre tous les points (n), sauf le point considéré (-1) et SAUF les n-2 points déjà vu (-(n-2));

soit la formation de n – 1 – (n – 2) segments. Ce qui donne 1.

Le quatrième point, l'avant-dernier, donne 1 segment.

Le cinquième, le dernier, donne zéro, bien sûr.

SEGMENTS – Total et formule

Calcul de la quantité totale de segments

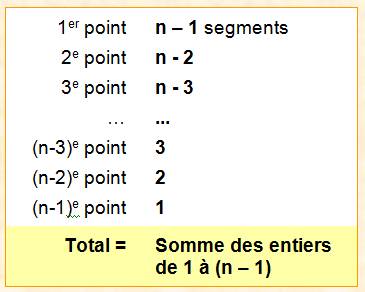
Formule de calcul

L'astuce consiste à les écrire DEUX fois: une fois en décroissant et une fois en croissant.

Et alors, la somme devient évidente comme par enchantement: chaque colonne donne une somme partielle égale à n et il y a n – 1 telles colonnes

Voici le calcul

DIAGONALES

Observation

Nous voici avec deux formules

s = n + d

s = n (n – 1) / 2

On peut calculer la quantité de diagonales

d = s – n

d = (n (n – 1) / 2) – n

d = n (n – 3) / 2

Conclusion

Exemples

Polygone	Côtés	Segments	Diagonales
	n	s = n (n – 1) / 2	d = n (n – 3) / 2
Triangle	3	3	0
Carré	4	6	2
Pentagone	5	10	5
Hexagone	6	15	9
Heptagone	7	21	14
Myriagone	1 000	499 500	498 500