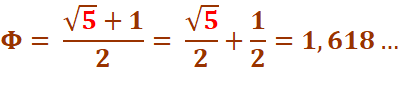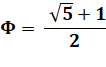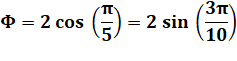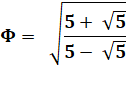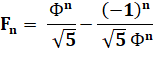|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
NOMBRE
d'OR et Nombre CINQ
L'expression la
plus connue contient le nombre 5, mais il y en a bien d'autres. |
|
Relations avec 5 |
|
|
|
|
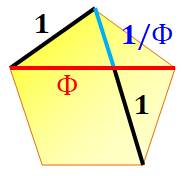
- Diagonales et côtés sont dans le
rapport du nombre d'or; et - Les diagonales se coupent selon la
section dorée (en bleu). Le plus petit des segments vaut 1 / phi, alors que
l'autre vaut 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
|
Suite |
|
|
Aussi |
|
|
DicoNombre |
|
|
Cette page |
![]()