NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 19/01/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Nombres
Débutants Géométrie	NOMBRE D'OR				Glossaire NOMBRE D'OR
Débutant		Valeurs	Phi et Fibonacci	Proportion
Tout PHI en bref		Formules	Puissances	Construction
Introduction		Fraction continue	Trigonométrie	Géométrie
Historique
	Sommaire de cette page >>> Historique >>> Modulor >>> Aujourd'hui >>> Mythe

NOMBRE D'OR

BIBLE >>>	Aucune référence au nombre d'or.
ÉGYPTE >>>	On prétend que: Le nombre d'or est présent dans certaines œuvres d'art de l'Égypte ancienne. Dans la grande pyramide de Gizeh, le rapport de l'altitude d'une face au demi côté de la base est presque exactement de 1,618 Le papyrus Rhind se réfère à un rapport sacré ?... Etc. Mais … Le nombre d'or n'est absolument pas connu des Égyptiens. Toutes les observations faites pour montrer que la proportion d'or existe ont été faites quelques millénaires après coup ! Une pyramide étant une tombe sacrée, il est plus que pensable que si un tel symbole, la proportion dorée, avait été utilisée, elle aurait été reportée dans les messages figurant dans les pyramides. Or, ce n'est pas le cas. Le système de mesure était essentiellement basé sur les parties du corps. Il n'est pas étonnant de retrouver dans les édifices les mêmes proportions que celles que l'on pourrait observer sur le corps humain.
GRECS	École de pensée du mathématicien grec Pythagore au - IVe siècle (-570 / -480) qui dit que "  tout est arrangé selon le nombre " Pythagore et ses disciples font la découverte des segments incommensurables sans doute en s'appuyant sur la proportion d'or. Euclide (325 – 265 av. J.-C.) définit la proportion correspondant au nombre d'or dans les " Éléments de géométrie " au III^e siècle Euclide constate l'existence d'un partage en extrême et moyenne raison, s'en sert, mais n'en fait nullement le centre de ses préoccupations – Marguerite Neveux Rien, sous la plume d'Euclide, ne rattache cette opération géométrique à quoi que ce soit d'esthétique ou de divin – Hannah Gabriel Les Grecs utilisaient probablement la proportion dorée en architecture, mais il n'en reste aucune preuve. Coïncidences ? Vitruve, architecte romain du 1^er siècle av. J.-C. , auteur de De Architectura (entre 30 et 15 av. J.-C. ). Il y aborde l'importance du dimensionnement proportionnel en architecture. Pas de référence au nombre d'or mais seulement à l'observation des proportions du corps humain.

MOYEN-ÂGE

Beaucoup tentent de trouver le partage euclidien dans les églises ou autres cathédrales de cette époque. Fibonacci (Leonardo Pisano: 1175 – 1250) est associé à ces tentatives. Il connaissait certainement cette proportion euclidienne. Il est vrai que Fibonacci est mathématiquement lié au nombre: le rapport entre deux nombres de Fibonacci successifs tend vers le nombre d'or. Cette suite, conduisant au nombre d'or, est magique. L'ensemble touche "au secret de la création, la mise en relation entre Dieu et les mathématiques" (Hannah Gabriel)

RENAISSANCE

Le partage euclidien est repris par le moine franciscain italien Fra Luca Pacioli, dit Luca di Borgo (né en 1445) dans " De divina proportione " (rédigé en 1498, publié en 1509), illustré par Léonard de Vinci. Il s'extasie devant l'ingéniosité du " partage en extrême et moyenne raison " (En géométrie, raison veut dire proportion) et en décrit ce qu'il nomme les treize effets. C'est un traité purement mathématique. Rien sur le plan esthétique ou artistique. Léonard de Vinci réfléchit aux proportions idéales du corps humain, basées sur le nombre d'or qu'il désigne par " sectio aurea " En 1492, Léonard de Vinci réalise le fameux "Homme vitruvien" qui illustrerait la divine proportion. Il mentionne la divine proportion dans son Traité de Peinture. Par contre, la recherche de cette proportion dans les œuvres de Leonardo fait souvent appel à des soustractions douteuses d'éléments dans les toiles. Il ne fait aucun doute que ce nombre fut consciencieusement exploité par les artistes de la Renaissance; nombre que Léonard nomma la divine proportion. L'édition italienne du "de Architectura" de Vitruve utilise le nombre d'or pour analyser la façade de la cathédrale de Milan. La proportion divine ou dorée est symbolisée par le dodécaèdre, synthèse géométrique de cette relation. Le dodécaèdre rassemble 12 pentagones. Johannes Kepler (1571- 1630) recherche Dieu dans la proportion divine.

XX^e SIÈCLE >>>

Martin Ohm (mi-1800), mathématicien allemand, parle de "der goldene Schnitt", la section d'or. Gustav Teodor Fechner (1801-1887): suite à diverses expériences il conclu qu’il existe une préférence naturelle pour la section d’or. "Après plus d’un siècle d’études, il est admis que l’hypothèse de Fechner est fausse et que le nombre d’or ne possède aucune qualité esthétique intrinsèque. Tenter d’expliquer l’harmonie est une tâche complexe qui nécessiterait un apport des neurosciences" – Nicoletta Sala (mathématicienne spécialités de la théorie du chaos et de la complexité) Adolf Zeising (1868) donne une valeur de perfection esthétique à la section d'or dans son ouvrage "das Pentagramm" Nombreux sont ceux qui à sa suite tenteront de voir la section d'or un peu partout. Ces écrits seront pris comme pain bénit par la suite et contribueront à la création de la légende sur le nombre d'or. 1932, naissance du " nombre d'or ", baptisé par un prince roumain, Matila prince Ghyka, qui tente de montrer qu'il existe une esthétique scientifique. Pour affirmer que le nombre d'or est la clef mathématique de la beauté, il se fonde sur le pentagone dont les diagonales forment une section dorée. En 1931, il publie: "Nombre d'Or. Rites et rythmes pythagoriciens dans le développement de la civilisation occidentale". Paul Valéry qui en rédigea la préface, contribua à populariser le nombre d'or jusqu'à la frénésie. Il "profite" largement des élucubrations historiques du siècle précédent ! Théodore Andrea Cook, journaliste, publie en 1914, un ouvrage sur les courbes de la vie tout en explorant le travail de Léonard de Vinci. C'est lui qui nomme le nombre d'or par la lettre grecque PHI majuscule (F) en hommage au sculpteur grec Phidias. Il fut émerveillé par sa visite du Parthénon à Athènes, dont la construction (447 – 432 av. J.-C.) a été dirigée par Phidias Il indique que le Parthénon aurait une proportion dorée… C'est vrai, mais à condition de supprimer sa première marche ! Léger, Kupka, Duchamp, Jacques Villon, les artistes de la Section d’or voient ce nombre comme la porte d'harmonie. Le Corbusier (1946) y découvre le secret d'une construction en série en inventant le Modulor, système de proportions architecturales pour harmonie et rapidité de construction. Plusieurs des réalisations majeures de l’architecte et urbaniste comme la Cité radieuse de Marseille ou la ville de Chandigarh en Inde sont basées sur le Modulor. Salvador Dali utilise le rectangle d'or dans son tableau : " demi - tasse géante volante, avec annexe inexplicable de cinq mètres de longueur ". Il a peint "Le Sacrement de la dernière cène" (1955) sur un tableau aux proportions du nombre d’or. Giorgo Griffa, peintre italien a qui le Centre d'art contemporain de Genève a consacré une rétrospective en 2015, s’est lui aussi intéressé au nombre d’or.

Modulor

Mot-valise formé avec module et nombre d'or.

Notion d'architecture inventée (1943) par Le Corbusier (1887-1965). Publication de Modulor 1 en 1948 et Modulor 2 en 1955.

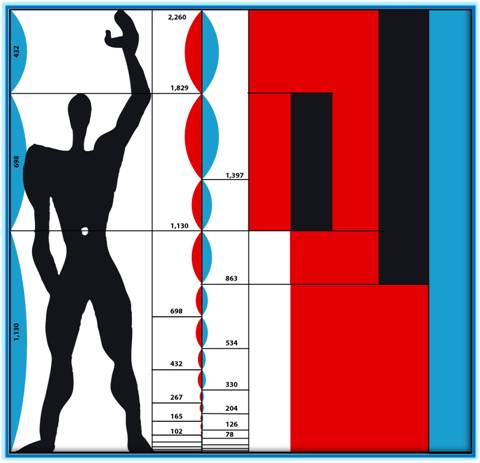
The Modulor: an harmonious measure to the human scale universally applicable to architecture and mechanics.

Dessin représentant une silhouette humaine standard dont les proportions harmonieuses s'appuient sur le nombre d'or.

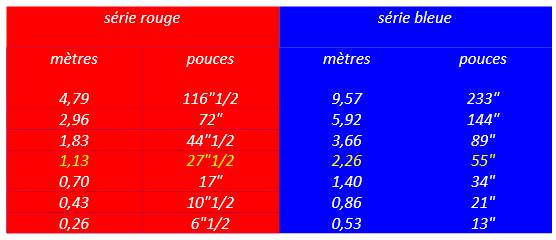
Le Corbusier nomme série rouge la suite de Fibonacci établie sur

l'unité de 1,13m et série bleue celle établie sur son double 2,26m.

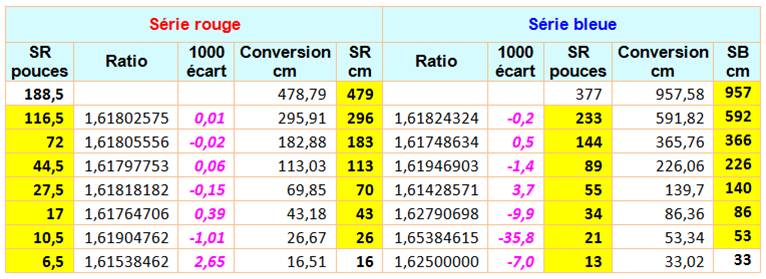
Analyse des deux jeux de séries par rapport au nombre d'or (1,618 033 988).

En jaune, les chiffres du tableau classique montré ci-dessus.

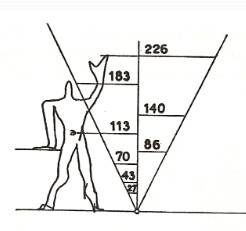
Exemple de lecture: 183 cm (72 ") et 113 cm (44,5 ") => ratio 72 / 44,5 = 1,6179…; différence avec le nombre d'or: 0,06 millième. 72" = 182,88 cm arrondi à 183.
La série bleue (SB) en pouces est exactement le double de la série rouge. Ex: 233 = 116,5 x 2.

Les mesures du corps humain en cm (reprise des nombres des séries bleue et rouge):

Einstein à propos du modulor: C'est un langage des proportions qui rend compliqué le mal et simple le bien.

Personnel: J'ai démarré mes études d'ingénieur en 1965. Ma promotion fut nommée Le Corbusier en l'honneur de cet illustre architecte décédé le 27 août 1965.

Aujourd'hui – 2010

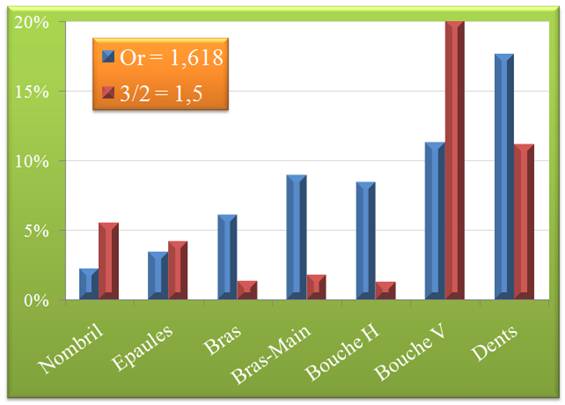
Nombreux sont ceux qui revendiquent une proportion harmonieuse, magique, voire religieuse en considérant le nombre d'or. Chirurgie esthétique Remodelage des parties du corps, spécialement la face, en tenant que les proportions du corps humain sont idéales de beauté lorsqu'elles reflètent le nombre d'or. Pour se donner une idée, voici un exemple typique pour lequel les proportions sont comparées au nombre d'or (1,618) et à la fraction 3/2 (1,5). Nombril = sol-nombril / nombril – haut du crâne Épaules = largeur d'épaule / épaule à coude Bras = épaule à coude / avant-bras Bras-main = avant-bras / longueur de main Bouche H = largeur de bouche au repos / largueur de nez Bouche V = menton-bouche / bouche-nez Dents = largueur incisive médiane / largeur incisive latérale Conclusions: ces rapports sont proches de 1,5 à 1,6; par contre impossible de conclure s'ils sont plutôt convergents vers le nombre d'or ou vers le rapport 3/2. Religion Affirmation que la Mecque, par volonté divine, est situé sur le nombre d'or du monde. Les proportions utilisées sont du type: rapport des distances aux pôles: 12 348,32 / 7 631,68 = 1,61803… Les mesures en km sont effectivement de cet ordre: 12 404 / 7 632 = 1,625 rapport des distances en longitude; rapport des distances sur la ligne de solstice; etc.

Voir les sites proposant des vidéos sur ces sujets

LE MYTHE DU NOMBRE D'OR

Le nombre d'or au XIX^e et XX^e siècles aurait exercé une fascination certaine. Sans doute du même type que celle connue lors de la recherche de la pierre philosophale.

Quel est le principe qui à lui seul résumerait le fonctionnement de l'Univers?

Marguerite Neveux

Université de Paris I - publie un livre:

" le nombre d'or, radiographie d'un mythe "

Elle y montre que, à partir de 1932, les adeptes du nombre d'or dissèquent et martyrisent les œuvres d'art pour y débusquer le nombre magique.

En fait, on trouve plutôt l'usage fréquent d'une proportion banale par les architectes et les artistes 5/8 = 0,625, proche de l'inverse du nombre d'or 0,618.

Il semble donc que le nombre d'or ne soit pas vraiment répandu avant Le Corbusier qui, lui, croyait au pouvoir de ce nombre.

Hannah Gabriel

Doctorat en sciences humaines.

"Le nombre d'or –

Histoire et symboles dans les religions, les arts et les sciences"

En 2005, elle approfondit cette thèse du mythe:

Depuis la renaissance et jusqu'au XX^e siècle, les hommes ont associé ce qui n'était qu'un théorème géométrique à toutes les formes de cultes de religions aussi loin qu'ils étaient en mesure de remonter dans le temps.

Pourtant:

aucune trace historique de la divine proportion en Égypte et Grèce antiques.

pour faire valoir la proportion, il faut amputer les édifices de certains morceaux

Certes, la proportion mathématique existe, bien entendu.

Par contre son caractère divin est réfuté, car non attesté: son caractère sacré est une injure à la réflexion logique ! dit-elle.

Matila Ghyga, à l'origine de la légende moderne, a signé un ouvrage intéressant témoin d'une quête, mais ses méthodes n'étaient pas pertinentes.

Les petits arrangements pour aboutir à sa théorie n'ont rien de scientifiques.

Il s'est tout simplement fabriqué un mythe qui a su se développer sur un terrain favorable.

 Toute cette page a été revisitée en 2006 en s'appuyant sur le livre de Hanah Gabriel

Merci à Guy Hekimian pour sa relecture attentive

Suite	Valeurs du nombre d'or Divine proportion
Aussi	Cercle Constante Pi Constantes Mathématiques Série du type Fibonacci et cousins Inventions – Chronologie Savants – Chronologie
DicoNombre	Nombre 1,618…
Livres	Le nombre d'or – Histoire et symboles dans les religions, les arts et les sciences – Hannah Gabriel – Éditions de Vecchi – 2005 Le nombre d'Or. Radiographie d'un mythe – Marguerite Neveux – éditions du Seuil - 1993
Sites de :	Eric Weisstein - mathworld.wolfram.com Golden Ratio Fibonacci Number Logarithmic Spiral
Autres sites	Le nombre d'or Le nombre d'or Le modulor par Bluteau David (pdf) Le Modulor : ultime résurgence du mythe ? Le mythe du nombre d'or – Sylvain Menétrey – 20 juillet 2017
Autres sites en anglais	Golden number Golden ratio links
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Geometri/NbOrHisto.htm