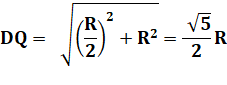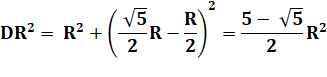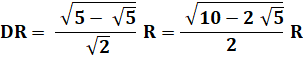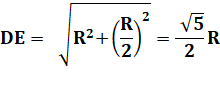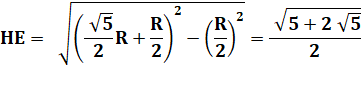NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 13/01/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Polygones
Débutants Géométrie	PENTAGONES				Glossaire Géométrie
INDEX Méthodes Constructions Polygones Géométrie	Général	Données	Constructions
	Pentagone	Mesures	Méthodes générales	Cercles – Mascheroni
	Nombre d'or	Angles	Avec Racine de 5	Approchée de Dürer
	Pentacle	Segments	Avec bissectrices	Approchée originale
			Méthode Euclide	Dissection
		Sommaire de cette page >>> 1) Construction règle et compas la plus connue >>> 2) Construction à partir de deux carrés >>> 3) Construction avec le nombre d'or >>> 4) Construction à partir d'un carré central >>> 5) Construction à partir d'un triangle équilatéral

PENTAGONE RÉGULIER – Constructions

impliquant la racine de 5

Plusieurs méthodes de construction du pentagone régulier dont celles basées sur la construction géométrique de la racine de 5 et nombre d'or.

1) Construction règle et compas la plus connue
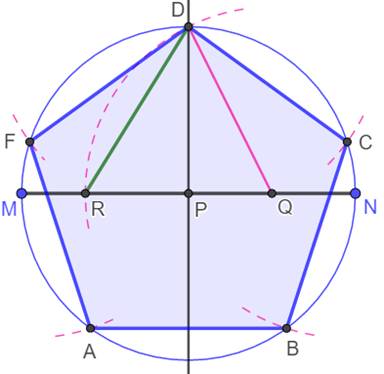
Construction dite de Ptolémée (vers 100-168) Réalisation d'un pentagone inscrit dans un cercle donné. Méthode basée sur l'utilisation de la racine de 5. Méthode classique que l'on trouvait dans les manuels de géométrie d'autrefois. Méthode Un segment MN. Son milieu P et Q le milieu de PN. Cercle de centre P et de rayon PN. Un diamètre perpendiculaire à MN. Intersection avec le cercle en D. Construction de la racine de 5 avec DQ Cercle de centre Q et de rayon QD. Intersection en R avec MN. La longueur du segment DR (en vert) est celle du côté du pentagone. Ouvrir le compas avec cet écartement et reporter cinq fois (quatre suffisent) cette longueur sur la circonférence du cercle Pentagone régulier: ABCDE.	Résumé: à partir de Q milieu de PN, cercle QD qui détermine R, alors DR représente le côté du pentagone.
Justification avec PM = PN = PD = R
Dans le triangle rectangle DPR:
DR est le côté du pentagone inscrit dans le cercle de rayon R.

2) Construction à partir de deux carrés
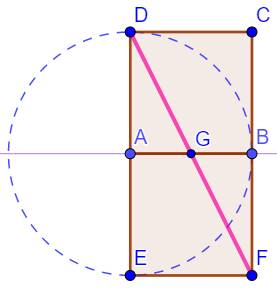
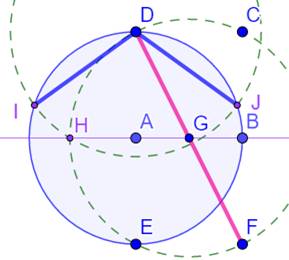
Construction avec deux carrés Réalisation d'un pentagone inscrit dans un cercle donné. Méthode basée sur l'utilisation de la racine de 5. Intérêt: trois points du pentagone sont tracés directement sur le cercle (sans report). Méthode Deux carrés ABCD et ABFE. La diagonale DF (introduisant la racine de 5). L'intersection G. Le cercle de centre A et de rayon AB sera le cercle circonscrit du pentagone. Cercle de centre G et de rayon GD. Intersection H. Cercle de centre D et de rayon DH. Intersections I et J. Cercle de centre I et de rayon ID. Intersection K. Cercle de centre J et de rayon ID. Intersection L. Pentagone régulier: IKLJD.

3) Construction avec le nombre d'or
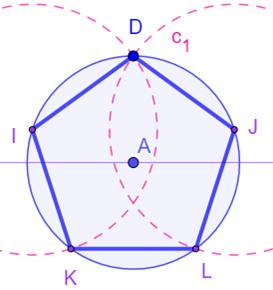
Construction avec le nombre d'or Réalisation d'un pentagone inscrit dans un cercle donné. On construit le nombre d'or puis les côtés du pentagone. Méthode

Merci à Jean-Marc P. pour avoir indiqué cette nouvelle élégante solution

4) Construction à partir d'un carré central
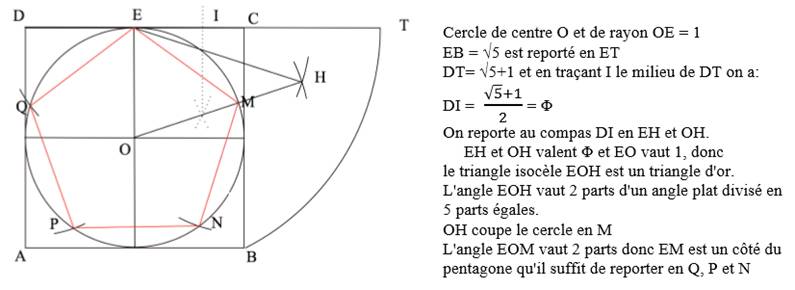
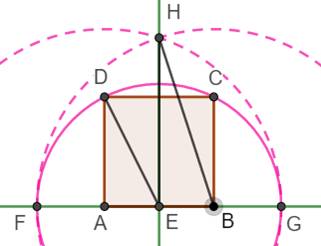
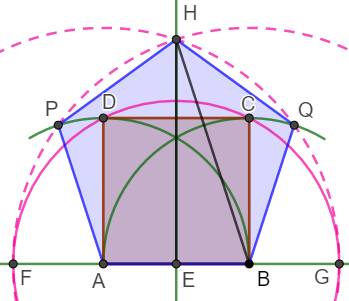
Construction avec un carré central Réalisation d'un pentagone dont un des côtés est le côté du pentagone. Rare méthode avec côté du pentagone comme point de départ. Méthode basée sur l'utilisation de la racine de 5. Le principe consiste à construire la hauteur HE du pentagone. Méthode On construit donc un carré ABCD sur le côté AB désiré pour le pentagone. Le cercle de centre E et de rayon ED coupe AB (prolongé) en F et G. Cercle de centre A et de rayon AG. Cercle de centre B et de rayon BF. Intersection en H, le sommet haut du pentagone. HE est une des hauteurs du pentagone. Cercle (vert) de centre A et de rayon AD. Intersection en P. Cercle (vert) de centre B et de rayon BC. Intersection en Q. Pentagone régulier: ABQHP.
Justificatif: segment DE avec DE² = AD² + AE²
Hauteur HE avec HE² = HB² – EB²

5) Construction à partir d'un triangle équilatéral
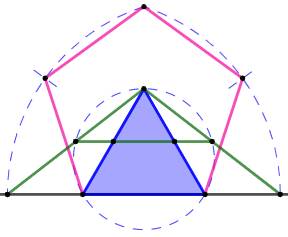
Construction Triangle équilatéral en bleu Son cercle circonscrit. Deux points milieux; segment vert. Suite de la construction et justification par Jean-Louis Breuil (pdf)

Retour	Méthodes de constructions – Introduction Pentagone
Suite	Construction avec les bissectrices et autres Pentagone et nombre d'or Pentacle Pentagone sous toutes les coutures Construction approchée du pentagone par la méthode Bion
Voir	Constructible Construction de l'icosagone Étoile à 6 branches Étoile et nombre d'or – Approche Fleurs à 5 pétales Géométrie – Bases Géométrie – Index Nombre d'Or Polygones
DicoNombre	Nombre CINQ
Sites	Voir les liens en première page
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Geometri/PentaCo1.htm