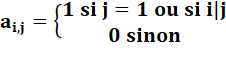|
Édition du: 10/04/2022 |
|
INDEX |
Types de Nombres – MODULO |
||||
|
1110
= 32 mod 71 |
|||||
|
|
|||||
Faites un double-clic pour un retour en haut de page
![]()
|
Triangles des modulos Signature d'un nombre par ses
modulos Une manière de voir
les nombres à travers leurs modulos. Une façon de voir qui distingue les nombres
composés des nombres
premiers. Le triangle des
modulos donne les valeurs des modulos alors que la matrice se limite à un
indicateur binaire de congruence. |
||
|
|
Sommaire de cette page >>> Approche >>> Triangle pour les nombres de 2 à 12 >>> Propriétés >>> TABLE pour les nombres de 2 à 100 >>> Matrice de Redheffer |
Débutants Glossaire |
Voir Triangle
de Pascal et autres
|
Cas d'un nombre n Prenons un nombre n = 10 et tous
les nombres premiers qui lui sont inférieurs: 2, 3, 5 et 7. On calcule n modulo ces premiers et on en fait
une liste. |
Calcul des modulos 10 mod 2 = 0 10 mod 3 = 1 10 mod 5 = 0 10 mod 7 = 3 Soit la liste 10 => [0, 1, 0, 3] |
|||||||||||||||||||||||||||||
|
Cas d'un nombre n Le calcul pour 11 donne la liste indiquée. |
Liste pour le nombre suivant 11 => [1, 2, 1, 4] |
|||||||||||||||||||||||||||||
|
Logique de passage de n a n + 1 On passe logiquement au suivant en ajoutant 1. |
|
|||||||||||||||||||||||||||||
|
Cas particuliers Pour 12, un nouveau nombre premier est à prendre
en compte. Par ailleurs, les sommes sont à pendre modulo le nombre
premier en tête de colonne. Une règle ? La signature modulo de n + 1 est aussi celle de n + 1 modulo le nombre premier de son rang. |
|
|||||||||||||||||||||||||||||
Merci à Rémy Aumeunier auquel j'ai emprunté
ce nom de signature
|
Composés ou premiers Un nombre premier est premier avec tous les nombres
premiers qui le précèdent. Sa signature est différente de 0 En revanche, un nombre composé présente toujours
au moins un zéro dans sa signature. |
|
|
|
Signature unique La signature de chaque nombre est unique (Les
lignes sont toutes différentes). Relation avec pi(n) La fonction pi(n) exprime la quantité de nombres
premiers inférieurs à n. C'est aussi la quantité de nombre non-nuls dans
la signature de n |
La signature de 12 est (2, 5, 1) soit trois
nombres. C'est aussi la quantité de nombres premiers qui
sont premiers avec 12. Seuls (2, 5 et 1) le sont. |
|||||||||||||
|
n, 1 si premier, pi(n), [signature] 2, 1, 1, [] 3, 1, 2, [1] 4, 0, 2, [0, 1] 5, 1, 3, [1, 2] 6, 0, 3, [0, 0, 1] 7, 1, 4, [1, 1, 2] 8, 0, 4, [0, 2, 3, 1] 9, 0, 4, [1, 0, 4, 2] 10, 0, 4, [0, 1, 0, 3] 11, 1, 5, [1, 2, 1, 4] 12, 0, 5, [0, 0, 2, 5, 1] 13, 1, 6, [1, 1, 3, 6, 2] 14, 0, 6, [0, 2, 4, 0, 3, 1] 15, 0, 6, [1, 0, 0, 1, 4, 2] 16, 0, 6, [0, 1, 1, 2, 5, 3] 17, 1, 7, [1, 2, 2, 3, 6, 4] 18, 0, 7, [0, 0, 3, 4, 7, 5, 1] 19, 1, 8, [1, 1, 4, 5, 8, 6, 2] 20, 0, 8, [0, 2, 0, 6, 9, 7, 3, 1] 21, 0, 8, [1, 0, 1, 0, 10, 8, 4, 2] 22, 0, 8, [0, 1, 2, 1, 0, 9, 5, 3] 23, 1, 9, [1, 2, 3, 2, 1, 10, 6, 4] 24, 0, 9, [0, 0, 4, 3, 2, 11, 7, 5, 1] 25, 0, 9, [1, 1, 0, 4, 3, 12, 8, 6, 2] |
26, 0, 9, [0, 2, 1, 5, 4, 0, 9, 7, 3] 27, 0, 9, [1, 0, 2, 6, 5, 1, 10, 8, 4] 28, 0, 9, [0, 1, 3, 0, 6, 2, 11, 9, 5] 29, 1, 10, [1, 2, 4, 1, 7, 3, 12, 10, 6] 30, 0, 10, [0, 0, 0, 2, 8, 4, 13, 11, 7, 1] 31, 1, 11, [1, 1, 1, 3, 9, 5, 14, 12, 8, 2] 32, 0, 11, [0, 2, 2, 4, 10, 6, 15, 13, 9, 3, 1] 33, 0, 11, [1, 0, 3, 5, 0, 7, 16, 14, 10, 4, 2] 34, 0, 11, [0, 1, 4, 6, 1, 8, 0, 15, 11, 5, 3] 35, 0, 11, [1, 2, 0, 0, 2, 9, 1, 16, 12, 6, 4] 36, 0, 11, [0, 0, 1, 1, 3, 10, 2, 17, 13, 7, 5] 37, 1, 12, [1, 1, 2, 2, 4, 11, 3, 18, 14, 8, 6] 38, 0, 12, [0, 2, 3, 3, 5, 12, 4, 0, 15, 9, 7, 1] 39, 0, 12, [1, 0, 4, 4, 6, 0, 5, 1, 16, 10, 8, 2] 40, 0, 12, [0, 1, 0, 5, 7, 1, 6, 2, 17, 11, 9, 3] 41, 1, 13, [1, 2, 1, 6, 8, 2, 7, 3, 18, 12, 10, 4] 42, 0, 13, [0, 0, 2, 0, 9, 3, 8, 4, 19, 13, 11, 5, 1] 43, 1, 14, [1, 1, 3, 1, 10, 4, 9, 5, 20, 14, 12, 6, 2] 44, 0, 14, [0, 2, 4, 2, 0, 5, 10, 6, 21, 15, 13, 7, 3, 1] 45, 0, 14, [1, 0, 0, 3, 1, 6, 11, 7, 22, 16, 14, 8, 4, 2] 46, 0, 14, [0, 1, 1, 4, 2, 7, 12, 8, 0, 17, 15, 9, 5, 3] 47, 1, 15, [1, 2, 2, 5, 3, 8, 13, 9, 1, 18, 16, 10, 6, 4] 48, 0, 15, [0, 0, 3, 6, 4, 9, 14, 10, 2, 19, 17, 11, 7, 5, 1] 49, 0, 15, [1, 1, 4, 0, 5, 10, 15, 11, 3, 20, 18, 12, 8, 6, 2] |
|
|
50, 0, 15, [0, 2, 0, 1, 6, 11, 16, 12, 4, 21, 19, 13, 9, 7, 3] 51, 0, 15, [1, 0, 1, 2, 7, 12, 0, 13, 5, 22, 20, 14, 10, 8, 4] 52, 0, 15, [0, 1, 2, 3, 8, 0, 1, 14, 6, 23, 21, 15, 11, 9, 5] 53, 1, 16, [1, 2, 3, 4, 9, 1, 2, 15, 7, 24, 22, 16, 12, 10, 6] 54, 0, 16, [0, 0, 4, 5, 10, 2, 3, 16, 8, 25, 23, 17, 13, 11, 7, 1] 55, 0, 16, [1, 1, 0, 6, 0, 3, 4, 17, 9, 26, 24, 18, 14, 12, 8, 2] 56, 0, 16, [0, 2, 1, 0, 1, 4, 5, 18, 10, 27, 25, 19, 15, 13, 9, 3] 57, 0, 16, [1, 0, 2, 1, 2, 5, 6, 0, 11, 28, 26, 20, 16, 14, 10, 4] 58, 0, 16, [0, 1, 3, 2, 3, 6, 7, 1, 12, 0, 27, 21, 17, 15, 11, 5] 59, 1, 17, [1, 2, 4, 3, 4, 7, 8, 2, 13, 1, 28, 22, 18, 16, 12, 6] 60, 0, 17, [0, 0, 0, 4, 5, 8, 9, 3, 14, 2, 29, 23, 19, 17, 13, 7, 1] 61, 1, 18, [1, 1, 1, 5, 6, 9, 10, 4, 15, 3, 30, 24, 20, 18, 14, 8, 2] 62, 0, 18, [0, 2, 2, 6, 7, 10, 11, 5, 16, 4, 0, 25, 21, 19, 15, 9, 3,
1] 63, 0, 18, [1, 0, 3, 0, 8, 11, 12, 6, 17, 5, 1, 26, 22, 20, 16, 10, 4,
2] 64, 0, 18, [0, 1, 4, 1, 9, 12, 13, 7, 18, 6, 2, 27, 23, 21, 17, 11, 5,
3] 65, 0, 18, [1, 2, 0, 2, 10, 0, 14, 8, 19, 7, 3, 28, 24, 22, 18, 12, 6,
4] 66, 0, 18, [0, 0, 1, 3, 0, 1, 15, 9, 20, 8, 4, 29, 25, 23, 19, 13, 7,
5] 67, 1, 19, [1, 1, 2, 4, 1, 2, 16, 10, 21, 9, 5, 30, 26, 24, 20, 14, 8,
6] 68, 0, 19, [0, 2, 3, 5, 2, 3, 0, 11, 22, 10, 6, 31, 27, 25, 21, 15, 9,
7, 1] 69, 0, 19, [1, 0, 4, 6, 3, 4, 1, 12, 0, 11, 7, 32, 28, 26, 22, 16, 10,
8, 2] 70, 0, 19, [0, 1, 0, 0, 4, 5, 2, 13, 1, 12, 8, 33, 29, 27, 23, 17, 11,
9, 3] 71, 1, 20, [1, 2, 1, 1, 5, 6, 3, 14, 2, 13, 9, 34, 30, 28, 24, 18, 12,
10, 4] 72, 0, 20, [0, 0, 2, 2, 6, 7, 4, 15, 3, 14, 10, 35, 31, 29, 25, 19,
13, 11, 5, 1] 73, 1, 21, [1, 1, 3, 3, 7, 8, 5, 16, 4, 15, 11, 36, 32, 30, 26, 20,
14, 12, 6, 2] 74, 0, 21, [0, 2, 4, 4, 8, 9, 6, 17, 5, 16, 12, 0, 33, 31, 27, 21, 15,
13, 7, 3, 1] 75, 0, 21, [1, 0, 0, 5, 9, 10, 7, 18, 6, 17, 13, 1, 34, 32, 28, 22,
16, 14, 8, 4, 2] 76, 0, 21, [0, 1, 1, 6, 10, 11, 8, 0, 7, 18, 14, 2, 35, 33, 29, 23,
17, 15, 9, 5, 3] 77, 0, 21, [1, 2, 2, 0, 0, 12, 9, 1, 8, 19, 15, 3, 36, 34, 30, 24, 18,
16, 10, 6, 4] 78, 0, 21, [0, 0, 3, 1, 1, 0, 10, 2, 9, 20, 16, 4, 37, 35, 31, 25, 19,
17, 11, 7, 5] 79, 1, 22, [1, 1, 4, 2, 2, 1, 11, 3, 10, 21, 17, 5, 38, 36, 32, 26,
20, 18, 12, 8, 6] 80, 0, 22, [0, 2, 0, 3, 3, 2, 12, 4, 11, 22, 18, 6, 39, 37, 33, 27,
21, 19, 13, 9, 7, 1] 81, 0, 22, [1, 0, 1, 4, 4, 3, 13, 5, 12, 23, 19, 7, 40, 38, 34, 28,
22, 20, 14, 10, 8, 2] 82, 0, 22, [0, 1, 2, 5, 5, 4, 14, 6, 13, 24, 20, 8, 0, 39, 35, 29, 23,
21, 15, 11, 9, 3] 83, 1, 23, [1, 2, 3, 6, 6, 5, 15, 7, 14, 25, 21, 9, 1, 40, 36, 30, 24,
22, 16, 12, 10, 4] 84, 0, 23, [0, 0, 4, 0, 7, 6, 16, 8, 15, 26, 22, 10, 2, 41, 37, 31,
25, 23, 17, 13, 11, 5, 1] 85, 0, 23, [1, 1, 0, 1, 8, 7, 0, 9, 16, 27, 23, 11, 3, 42, 38, 32, 26,
24, 18, 14, 12, 6, 2] 86, 0, 23, [0, 2, 1, 2, 9, 8, 1, 10, 17, 28, 24, 12, 4, 0, 39, 33, 27,
25, 19, 15, 13, 7, 3] 87, 0, 23, [1, 0, 2, 3, 10, 9, 2, 11, 18, 0, 25, 13, 5, 1, 40, 34, 28,
26, 20, 16, 14, 8, 4] 88, 0, 23, [0, 1, 3, 4, 0, 10, 3, 12, 19, 1, 26, 14, 6, 2, 41, 35, 29,
27, 21, 17, 15, 9, 5] 89, 1, 24, [1, 2, 4, 5, 1, 11, 4, 13, 20, 2, 27, 15, 7, 3, 42, 36, 30,
28, 22, 18, 16, 10, 6] 90, 0, 24, [0, 0, 0, 6, 2, 12, 5, 14, 21, 3, 28, 16, 8, 4, 43, 37, 31,
29, 23, 19, 17, 11, 7, 1] 91, 0, 24, [1, 1, 1, 0, 3, 0, 6, 15, 22, 4, 29, 17, 9, 5, 44, 38, 32,
30, 24, 20, 18, 12, 8, 2] 92, 0, 24, [0, 2, 2, 1, 4, 1, 7, 16, 0, 5, 30, 18, 10, 6, 45, 39, 33,
31, 25, 21, 19, 13, 9, 3] 93, 0, 24, [1, 0, 3, 2, 5, 2, 8, 17, 1, 6, 0, 19, 11, 7, 46, 40, 34,
32, 26, 22, 20, 14, 10, 4] 94, 0, 24, [0, 1, 4, 3, 6, 3, 9, 18, 2, 7, 1, 20, 12, 8, 0, 41, 35,
33, 27, 23, 21, 15, 11, 5] 95, 0, 24, [1, 2, 0, 4, 7, 4, 10, 0, 3, 8, 2, 21, 13, 9, 1, 42, 36,
34, 28, 24, 22, 16, 12, 6] 96, 0, 24, [0, 0, 1, 5, 8, 5, 11, 1, 4, 9, 3, 22, 14, 10, 2, 43, 37,
35, 29, 25, 23, 17, 13, 7] 97, 1, 25, [1, 1, 2, 6, 9, 6, 12, 2, 5, 10, 4, 23, 15, 11, 3, 44, 38,
36, 30, 26, 24, 18, 14, 8] 98, 0, 25, [0, 2, 3, 0, 10, 7, 13, 3, 6, 11, 5, 24, 16, 12, 4, 45, 39,
37, 31, 27, 25, 19, 15, 9, 1] 99, 0, 25, [1, 0, 4, 1, 0, 8, 14, 4, 7, 12, 6, 25, 17, 13, 5, 46, 40,
38, 32, 28, 26, 20, 16, 10, 2] 100, 0, 25, [0, 1, 0, 2, 1, 9, 15, 5, 8, 13, 7, 26, 18, 14, 6, 47, 41,
39, 33, 29, 27, 21, 17, 11, 3] |
||
|
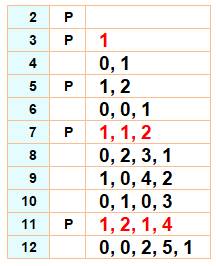
Matrice On rappelle qu'une matrice
et un simple tableau de nombres. Ici, elle sera carrée: autant de lignes que de
colonnes. Matrice de Redheffer Elle caractérise la congruence des nombres. La valeur de chaque terme se calcule de cette
manière: Lecture: le terme en ligne i et colonne j est
égal à 1 pour la colonne où j = 1 ou partout ou i divise j; sinon, il vaut 0. |
Exemple avec matrice 3 x 3
La matrice est symétrique par rapport à la
diagonale descendante. La seule valeur nulle est pour 2 qui ne divise
par 3 (ou 3 qui ne divise par 2). |
|||||||||||||||||
|
Matrice de Redheffer pour n de 4 à
10
|
||||||||||||||||||
Voir Programmation des
matrices avec Maple
Bilan
|
Le triangle des modulos comme la matrice de Redheffer ont des
applications en théorie des nombres: sur la fonction de Mertens
ou encore la valeur propre
(eigenvalue). |
![]()
|
Retour |
|
|
|
Suite |
|
|
|
Voir |
|
|
|
Sites |
|
|
|
Cette page |
||