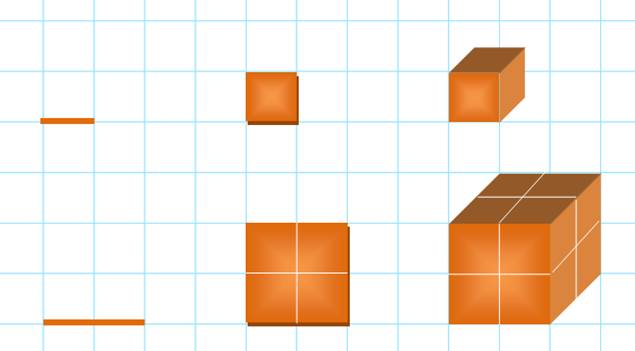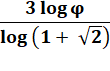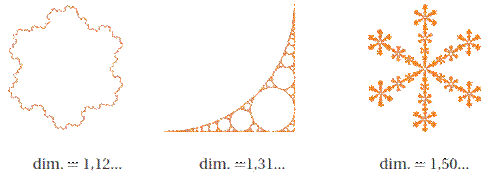|
|||||||||||||||||||||||||||||
![]()
|
FRACTALES
|
|
|
|
|
|
|
|
|
|
|
DIMENSION
TOPOLOGIQUE
0 – Point 1 – Courbe 2 – Surface 3 – Volume 4 – Hyper volume
Dimension
1 Dimension 2 Dimension 3 Segment
doublé Carré doublé Cube doublé Facteur
2 = 21 Facteur
4 = 22 Facteur
8 = 23
2Dimension
Topologique C'est encore une valeur entière |
|
Voir Duplication du cube
|
|
|
|
Exemple
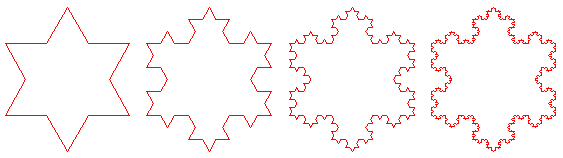
La dimension fractale du flocon est 1,26.
Définition Dimension fractale: log p / log q Avec q facteur
d'agrandissement p nombre de
fractales obtenues. Exemple
Dimension fractale: log 4 / log 3 = 1,26… Voir Logarithmes Définition
précise
Valeur de d pour laquelle le
volume de dimension d change de l'infini à zéro.
Approche
de cette définition
Dimension
fractale D
|
|
|
|
|||
|
Objet |
Dimension |
Formule |
|
|
0,6309297534 |
log 2 /
log 3 |
||
|
|
1,261859507 |
log 4 /
log 3 |
|
|
1,3057 |
|
||
|
1, 333 |
4/3 |
||
|
1,33?
(<1,5) |
Constat |
||
|
|
1,584962501 |
log 3 /
log 2 |
|
|
1,637938208… |
|
||
|
1,7 |
|
||
|
|
1,7 |
|
|
|
|
1,7227 |
log 16 /
log 5 |
|
|
|
1,86171596 |
log 6 /
log ( 2 / (3- |
|
|
|
1,892789260 |
log 8 /
log 3 |
|
|
|
2 |
Pas
réellement des fractales |
|
|
|
2,5 |
|
|
|
|
2,5 |
|
|
|
|
2,726833027 |
log 20 /
log 3 |
|
|
Objet de dimensions 0 ou 1 |
Point
Ligne
ouverte ou fermée |
|
|
Objets fractals |
1890, Giuseppe Peano
(1858-1932): il existe des courbes qui remplissent complètement toute la
surface d’un carré, c’est-à-dire des courbes si tortueuses qu’elles couvrent
sans la moindre lacune tout le carré. |
|
|
Construction |
Réaliser
par itération une suite de figures dont l’aire s’amenuise par évidements
successifs, jusqu’à l’annulation pour une répétition infinie. |
|
|
Exemple des pentagones Un
assemblage de pentagones. L’opération
consiste à remplacer chaque pentagone par une réduction appropriée de la
figure de départ Exemple de triangles |
|
|
|
Dimension fractale Toutes
ces figues fractales ont une aire nulle. La
densité des traits est de plus en plus importante. Elle
est caractérisée par la dimension fractale de la figure. Une
notion qui témoigne du repliement des figures lors d'une itération. |
|
|
Voir Solution de Besicovitch pour le
problème de l'aiguille
|
|
|
|
2,502 908… et
4,669 201 66… = Valeurs de Feigenbaum Valeur
d'étirement des
figures fractales.
Dans
le cas de certaines courbes fractales,
Cette
propriété est valable
Keith
Briggs du département
mathématiques de l'université de Melbourne détient le record du calcul de
décimales: 4,6692016091
0299067185 3203820466 2016172581 8557747576 8632745651 3430041343 3021131473
7138689744 0239480138 1716598485 5189815134 4086271420 2793252231 2442988890
8908599449 3546323671 3411532481 7142199474 5564436582 3793202009 5610583305
7545861765 2222070385 4106467494 9428498145 339172620 0568755665 9523398756
0382563722 5 |
|
Voir Constante
de Feigenbaum et dédoublement / Nombres
de Feigenbaum transcendants
![]()
|
Suite |
|
|
Voir |
|
Sites |
|
|
Cette
page |
![]()