|
|||||||||||||||||||||||||||||||||||
![]()
|
Coloration des graphes avec trois couleurs Coloration d'une carte
simple avec combien de couleurs? Preuve que trois ne suffit
pas dans le cas général. Et si la carte ne comportait
que des triangles? Mais quelles sont les
conditions pour la carte puisse être coloriée avec seulement trois couleurs?
C'est un problème très ardu! Typiquement deux et trois couleurs
|
Actualités Juin 2016 – Cas où trois couleurs
suffiraient
|
En 1976, les Américains Kenneth Appel et Wolfgang Haken démontrent
le théorème des quatre couleurs. La même année, Richard Steinberg conjecture que
trois couleurs suffisent pour tout graphe
planaire sans cycle de longueurs 4 ou 5 (boucles comprenant 4 ou 5
sommets, chacun représentant une région à colorier). Steinberg's conjecture: Every planar graph without 4-cycles and 5-cycles is 3-colourable. En 2005, Oleg Borodin (Russie) et ses collègues ont montré
que trois couleurs suffisent pour les graphes dépourvus de cycles de 4, 5, 6
et 7 nœuds. En avril 2016,
Vincent Cohen-Addad (École supérieure de Paris) ont trouvé un graphe sans
cycle 4 ou 5 impossible à colorier
avec trois couleurs. La conjecture de Steinberg est fausse.
|
D'après Colorier
des cartes avec seulement trois couleurs – Sean Bailly – Pour la Science –
Juin 2016
Publication des auteurs
(anglais)
|
|
|
|
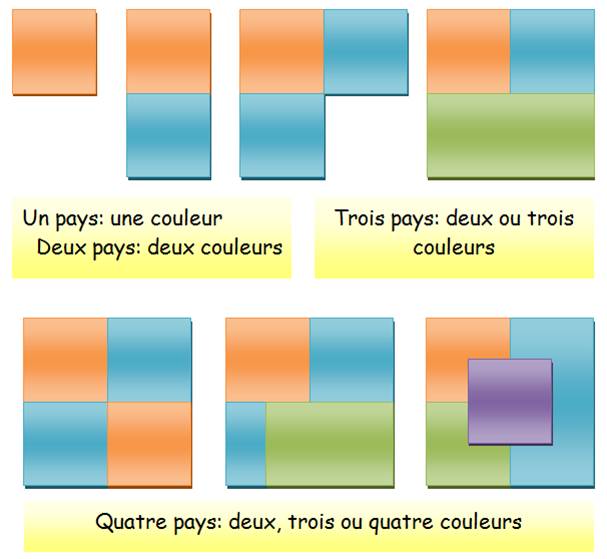
Une carte comporte un pays, deux pays, trois pays ou
quatre pays: combien faut-il de couleurs? Nous rappelons que le jeu consiste
à ce que deux pays partageant une frontière soient colorés de deux couleurs différentes.
Le dernier cas (en bas, à droite) montre que le cas
général exige au moins quatre couleurs. Une autre manière de la voir:
On note que dans ce cas, la règle est respectée y
compris en incluant le fond de carte. Cherchez bien! Personne n'a pu trouver un cas qui nécessite
cinq couleurs. |
|
|
|
||
|
Partition du plan en
triangles tel que deux triangles
|
Les trois cas recevables et, à droite, un cas non valable |
|
|
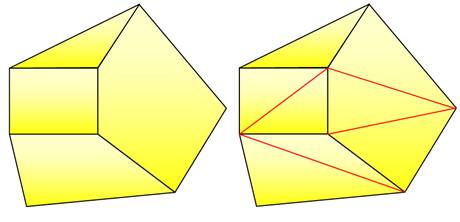
Il est toujours
possible de trianguler une région en
dessinant des diagonales. La quantité d'arêtes est augmentée
sans que n'augmente la quantité de sommets. |
|
|
|
Si une carte triangulée
(plane) est 4-coloriable, alors la carte d'origine est 4-coloriable. Il suffit donc de prouver le
théorème des quatre couleurs pour des cartes triangulées. La recherche de la
triangulation avec un minimum d'arêtes ajoutée est un problème de type
NP-Complet. |
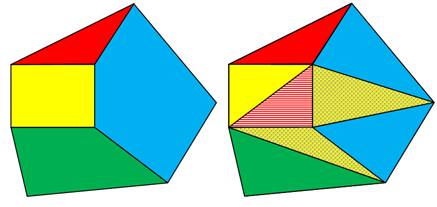
Certaines parties de la face conservent leur couleur.
Les trois triangles recolorés sont montrés en hachuré. |
|
|
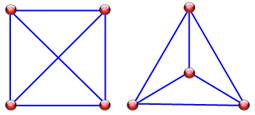
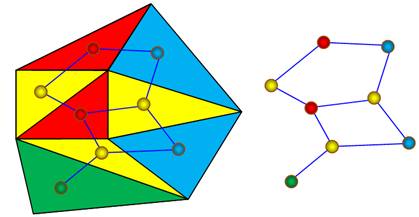
Le passage au graphe montre
des sommets de degré maximum égal à 3. S'ils sont tous à 3, le
graphe est dit cubique. |
|
|
|
On pourrait penser que 3
arêtes conduit à trois couleurs … pas toujours vrai. |
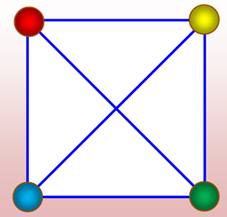
Théorème de Brooks Un grapghe cubique est 3-coloriable,
sauf dans le cas du graphe complet K4
|
|
|
|
||
|
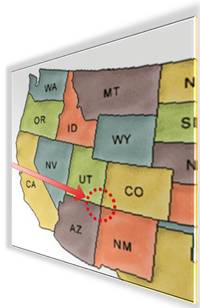
Si un sommet présente:
Dans le cas de la carte des États-Unis, seuls les États
indiqués par la flèche présentent un sommet quadruple. |
Cas
d'un sommet de degré 5
Cas
de la carte des E.-U.
|
|
|
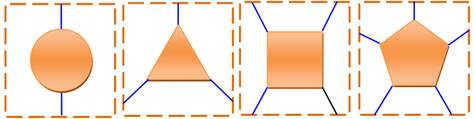
Toute
carte peut être triangulée rendant le problème plus facile à résoudre. Si
cette carte est 4-coloriable, alors la carte originelle l'est aussi. Toute
carte triangulée contient au moins un des quatre configurations inévitables suivantes:
|
|
|
||
|
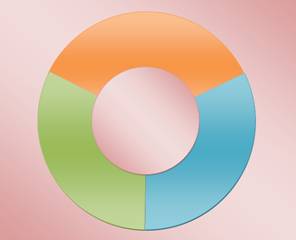
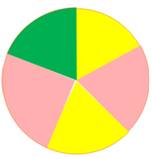
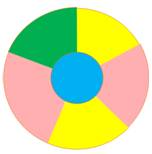
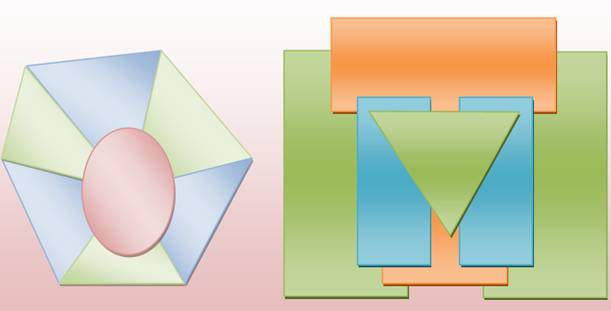
Exemples de zones colorées avec seulement
trois couleurs. Notez que sur la figure de gauche chaque région est entourée
d'un nombre pair de régions (hors région de fond). La figure de droite
introduit des zones incluses (des îles) qui compliquent le problème.
Kempe en 1879 était
sur cette piste de quantité paire de régions. Il avait bien pensé Voyez cet exemple. Chaque région côtoie un nombre
pair de régions et pourtant sa coloration impose quatre couleurs sommets
verts se font face! Alors, une quatrième couleur est nécessaire. La condition nécessaire
et suffisante pour trois couleurs est un problème ardu. Il s'agit même
d'un problème NP-complet
selon la démonstration de Stockmeyer. Par contre, il existe des conditions suffisantes pour trois couleurs, comme le
théorème de Grötzsch qui dit qu'il suffit que le graphe soit planaire sans
présence de triangle. Un cas particulier: si toutes les faces sont des
triangles, la condition nécessaire et suffisante est que chaque sommet soit
de degré pair.
|
||
|
Théorème
d'Erdös Pour tout k, il existe un graphe sans triangle qi
nécessite au moins k couleurs. |
k
= 3 Un graphe planaire sans triangle est 3-coloriable. |
|
Voir la transposition en graphe
![]()
|
Retour Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Topologi/aaaGraph/Coul3.htm
|
![]()