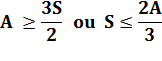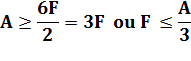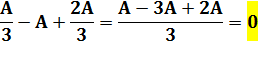|
|||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Cas de CINQ COULEURS En voulant démontrer les
quatre couleurs, Kempe
avait finalement réussi à démontrer le cas de cinq couleurs. |
|
|
|
|
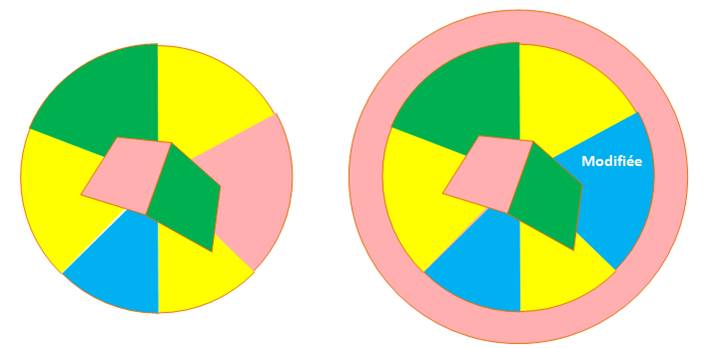
La carte est colorée avec
quatre couleurs, la région suivante entoure les quatre. Comment faire? Ici,
il est possible de modifier l'une des couleurs.
|
|
|
|
|
|
Colorier une carte quelconque avec cinq
couleurs est toujours assez facile. Un exemple permet de toucher du doigt la
difficulté de démontrer que quatre est suffisant. Soit le dessin suivant
Cet exemple illustre le fait que: il
n'existe pas de configurations pour lesquelles chacune des cinq régions
partage une frontière commune avec les quatre autres. Nombreux sont ceux qui
ont conclu à tord que, puisque cinq régions ne pouvent
jamais être adjacentes aux quatre autres, alors quatre
couleurs suffisent. Conclusion Le nombre de couleurs n'est pas égal au
plus grand nombre de régions adjacentes. On ne peut pas utiliser une
telle implication, même si à première vue, elle paraît évidente. La démonstration
devra utiliser de nombreux artifices pour déjouer ce piège, et pour arriver à
quatre couleurs, il faudra examiner des milliers de
cas possibles par ordinateur.
|
|
|
|
|||
|
|
|
|
|
|
Difficulté
pour construire cinq régions chacune voisine des quatre autres
Graphe avec six sommets,
chacun raccordé aux cinq autres, sans croisement. Impossibilité démontrée
par De Morgan. |
|
||
|
Difficulté
de trouver cinq régions avec frontières communes
Pour introduire la cinquième, il
faut passer dans l'une des quatre autres. |
|
||
|
|
||
|
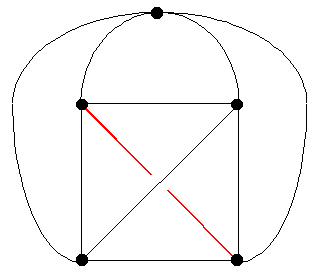
Théorème Il est impossible de disposer cinq
régions de telle façon qu'il existe des frontières communes entre tous les
couples possibles. Ou, aussi Il
n'existe aucune carte avec cinq pays, chacun jouxtant les quatre autres. Ou, équivalent Il
n’existe pas de graphe à cinq sommets de sorte que chaque sommet soit
connecté aux cinq autres sans branches qui se coupent. Illustration La
diagonale rouge coupe l’autre diagonale
|
Démonstration Un truc pour commencer On
ajoute une région au graphe, la région externe. La relation d’Euler devient: F – A + S = 2 Or, ici S = 5 A = 4 + 3 + 2 + 1 =
10 Avec
la relation d’Euler, le nombre de régions doit être F = A – S + 2 = 7 Deuxième évaluation Chaque
région est limitée par au moins trois arêtes. Soit, avec la conclusion
précédente, le graphe compte au moins: 7 x 3 = 21 arêtes. Chaque
arête limite deux régions. On a donc compté les arêtes deux fois. Il faut
diviser par 2: A > 21/2 A (Il n’y pas de ½
arête) Contradiction On
avait calculé seulement 10 arêtes et non 11. L’hypothèse
de départ est fausse Il
n’est pas possible de connecter cinq points sans recoupement. |
|
Voir Lois de De
Morgan en logique
|
|
||
|
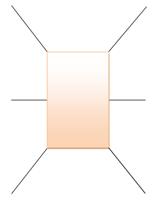
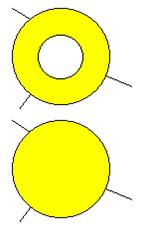
Toute carte contient au moins un pays qui à cinq voisins ou moins. Supposons une région avec
six voisins. Un calcul
arithmétique avec la relation d'Euler montre que ce n'est pas possible. Démonstration |
Exemple de région avec six
voisins
Forme complète et forme simplifiée |
|
|
Chaque sommet reçoit au
moins 3 arêtes, et chaque arête
connecte deux sommets. |
|
|
|
Supposons que la carte ne
comporte que des régions à six frontières ou plus. |
F régions (ou faces) avec plus de cinq
frontières. |
|
|
Si toutes les régions
avaient six arêtes (cas minimum), chaque arête bordant deux régions. |
|
|
|
En injectant ces valeurs
dans la relation d'Euler avec les valeurs minimales |
F – A + S = 2
|
|
|
L'invariant d'Euler n'est
pas respecté |
La contradiction montre que la carte de peut pas
ne contenir que des régions ayant six régions ou plus. |
|
Démonstration
alternative (même principe)
|
|
|
|
|
s = 2a / 3 |
|
|
s – a + f = 2 devient: 3f – a = 6 |
|
La formule commence par 2
car pas d'enclaves, ni d'îles. |
f = P2 + P3 + … + PN e = ½ (2P2 + 3P3 +… + N.Pn) |
|
|
4P2 + 3P3 + 2P4
+ P5 – P7 – 2P8 – 3P9 – …– (N – 6)PN = 12 |
|
|
Pn contribue positivement à la somme que si n vaut 2, 3, 4 ou 5. |
|
|
|
|
|
||
|
Théorème de Heawood
(1890) Cinq
couleurs suffisent
toujours pour colorier une carte sans région
adjacentes de la même couleur. Procédé de réduction Il
faut trouver un procédé qui n’altère pas le nombre maximum de couleurs. On a
dénombré un total de 6 cas. Intérêt Donner
un résultat tangible avec une preuve courte. |
Démonstration On
utilise encore le même truc. Il y a une région extérieure au graphe. On
imagine le graphe dessiné sur une sphère. Alors: F – A + S = 2 Méthode On
va réduire les régions de la carte de départ (quelconque) en associant deux
régions adjacentes. Et, ceci pour aboutir
à un graphe final de cinq régions seulement. Ainsi Le
graphe final nécessite cinq couleurs, au plus. |
|
Voir Démonstration
/ Historique
|
|
|||
|
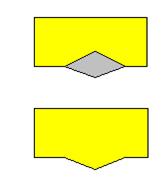
Cas 1 |
|
Dans
toute la suite, on suppose que le reste de la carte est résolu et que
subsiste ce type configuration. Valable pour toute la description
ci-dessous. Ici,
on fusionne la partie intérieure. Bilan
(évident), il faut deux couleurs. |
|
|
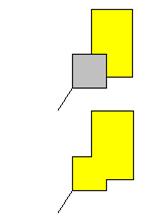
Cas 2 |
|
Sommet
avec plus de trois arêtes. Soit pus de quatre régions. Il existe une paire de
régions qui n'a pas de frontière commune. Elles fusionnent. On donne la même
couleur à cette nouvelle région. Tout coloriage initial de la carte n'est pas
modifié par cette opération. En
appliquant cette procédure, les sommets comportent au plus trois arêtes. |
|
|
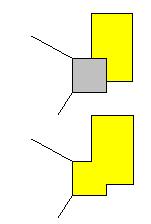
Cas 3 |
|
Région
limitrophe avec deux autres. On la fusionne avec l'une des deux. Si on peut
colorier la carte avec au moins trois couleurs, la nouvelle carte pourra,
elle aussi, être colorié avec trois couleurs. La partie "engloutie"
sera coloriée différemment des deux régions l'entourant. |
|
|
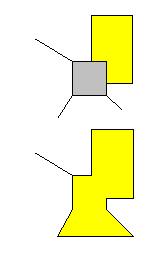
Cas 4 |
|
Une
région avec trois voisins. On fusionne avec l'un d'entre eux. Si la nouvelle
carte peut être coloriée avec quatre couleurs, la carte d'origine peut l'être
aussi. |
|
|
Cas 5 |
|
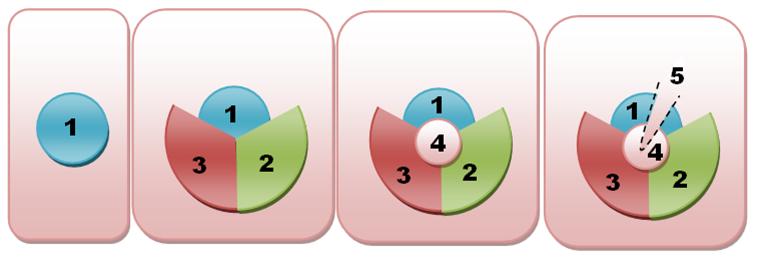
Une
région avec quatre voisins. On fusionne avec l'un d'entre eux. Si la nouvelle
carte peut-être coloriée avec cinq couleurs, la carte d'origine peut l'être
aussi. |
|
|
Cas 6 |
|
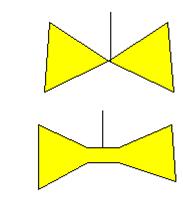
Une
région avec cinq voisins. Il existe une paire de régions qui ne se touchent
pas. On fusionne les trois. Si la nouvelle carte peut-être coloriée avec cinq
couleurs, la carte d'origine peut l'être aussi. Il
faut quatre couleurs pour la nouvelle carte: trois pour l'extérieur; une pour
la région fusionnée (jaune, ici). On
dé-fusionne en donnant la 5e couleur à la région centrale et en gardant
le jaune pour les deux régions séparées. |
|
Bilan |
|
Note Inutile
d'optimiser à moins de cinq couleurs Le
cas n° 5 de réduction impose les cinq couleurs. |
![]()
|
Retour Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Topologi/aaaGraph/Coul5.htm
|
![]()