NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 22/09/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Nombres
Débutants Addition	Variations sur les carrés				Glossaire Addition
INDEX PARTITION CARRÉS	Carrés	Chiffres répétés	Repdigits	Chiffres consécutifs
	Produits	66 x 67 …	66 x 99 …	Factorisation
	Sommes	Somme double	A² + kB²
	Différences	Propriétés	Écart 1, 2, …	Trouver la dif. des carrés
	Autres	Table 1 à 100	Repdigits	Table des Repdigits
		Curiosités	Tableau synthèse	a² – b² = c² – d²
		Chiffres	Concaténation
	Sommaire de cette page >>> Devinette >>> Chiffres répétés

CHIFFRES RÉPÉTÉS DANS LES CARRÉS

Quantité du même chiffre dans les carrés

7744 = 88² Seul carré de 4 chiffres ayant ses chiffres initiaux et finaux doublés.

1444 = 38² Seul carré de 4 chiffres ayant trois chiffres identiques.

Record de présence d'un chiffre dans les carrés jusqu'à n = 1 000 000 (sauf pour les 0)

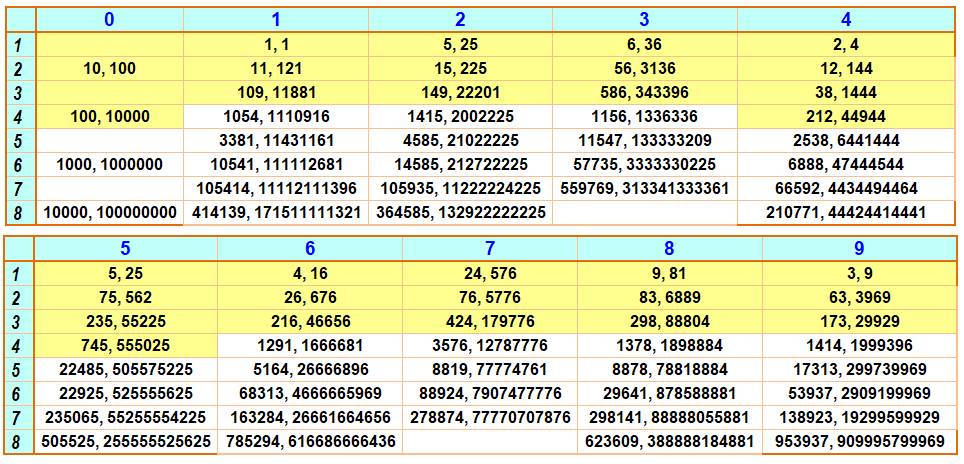
Voir Blocs de chiffres répétés

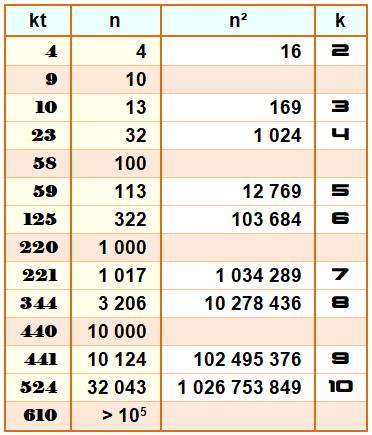
Plus petits nombres carrés à k chiffres distincts Colonne de gauche: kt quantité de tels carrés jusqu'à n, n étant le premier carré à k chiffres Lignes colorées: quantité de tels carrés jusqu'à une puissance de 10. Il existe seulement 610 carrés dont tous les chiffres sont distincts. Le plus grand carré à chiffres distincts est: 99 066² = 9 814 072 356 Voir Nombre 610

Voir Chiffres dans les carrés

DEVINETTE
Devinez un carré à quatre chiffres ayant ses deux premiers chiffres et ses deux derniers chiffres répétés. N = abcd avec a = b et c = d. La démonstration est intéressante.

On développe	n	= 1000a + 100b + 10c + d = 1000a + 100a + 10c + c = 100 x 11a + 11c = 11 (100a + c)
On constate que	n	est divisible par le nombre premier 11
Or n est un carré	n = u.u	= 11 (100a + c)
11 est l'un des facteurs premier de u	u	= 11k
Soit une nouvelle expression de n	n	= 11² k²
En égalant les deux formes de n	11 (100a + c)	= 11² k²
	100a + c	= 11 k²
Exprimons le premier facteur autrement	99a + a + c	= 11 k²
Soit la valeur de a + c	a + c	= 11 k² - 99a = 11(k² - 9a)
On constate que	a + c	est aussi divisible par 11
Il nous reste à explorer les diverses possibilités pour obtenir cette somme
D'abord a et c sont des chiffres	a + c	< 9 + 9 = 18
Ensuite c est le chiffre des unités d'un carré qui ne peut être que ^1	c	= {1, 4, 5, 6, 9}
Explorons
c = 1; a = 10		pas possible
c = 4; a = 7	n = 7744	= 88² BON
c = 5; a = 6	n = 6655	= 81,5…²
c = 6; a = 5	n = 5566	= 74,6…²
c = 9; a = 2	n = 2299	= 47,9…²
Seule solution	7744	= 88² = 8² x 11² = 2^6 x 11^2

Remarque

L'exploration peut être réduite en utilisant la propriété suivante: le carré d'un nombre impair produit une dizaine paire. Pour obtenir des chiffres unité et dizaine identiques, le carré doit être pair. Ce qui ramène l'exploration de c = {1, 4, 5, 6, 9} à seulement c = {4 et 6}.

Intérêt limité, mais beauté du recours à cette propriété.

CHIFFRES RÉPÉTÉS dans:

Carrés de 3 chiffres

n	n
121 144 225 441 484 676	11 12 15 21 22 26

Cubes de 3, 4 et 5 chiffres avec chiffres répétés

n	^3n
343 1331 2744 3375 29791	7 11 14 15 31

Carrés de 4 chiffres

n	n
1156 1225 1444 1521 1681 2116 3136 3364 3844 3969 4225 4489 4624 5625 5776 5929 6561 6889 7225 7744 8281 8464 8836	34 35 38 39 41 46 56 58 62 63 65 67 68 75 76 77 81 83 85 88 91 92 94

Carrés de 5 chiffres

n	n
11881 12321 14161 14641 16641 17161 19321 19881 25281 25921 29241 44521 48841 52441 53361 57121 68121 73441 77841 84681 94864	109 111 119 121 129 131 139 141 159 161 171 211 221 229 231 239 261 271 279 291 308

Suite	Chiffres répétés dans les carrés et les cubes (suite) Carrés et repdigits Nombres doublement carré Puissance concaténation de n puissances S'y retrouver
Voir	Addition - Glossaire Addition des carrés Addition des entiers Addition des puissances Carrés magiques Conjecture de Goldbach Demlo (Nombres -) Nombres consécutifs Identités remarquables Impairs Palindromes Repdigit Répétition de motifs
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Addition/P100a500/Carredig.htm