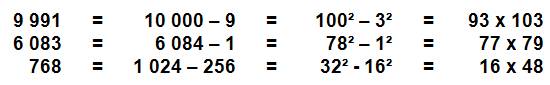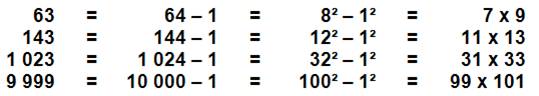NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 22/09/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Partitions
Débutants Addition	Variations sur les carrés				Glossaire Addition
INDEX PARTITION	Carrés	Chiffres répétés	Repdigits
	Produits	66 x 67 …	66 x 99 …	Factorisation
	Sommes	Somme double	A² + kB²	Factorisation – Algorithme
	Différences	Propriétés	Écart 1, 2, …	Trouver la dif. des carrés
	Autres	Table 1 à 100	Repdigits	Table des Repdigits
		Curiosités	Tableau synthèse	a² – b² = c² – d²
		Chiffres	Concaténation
		Sommaire de cette page >>> Méthode >>> Cas particuliers

FACTORISATION des nombres

différence de deux carrés

Observation des nombres qui peuvent se mettre sous la forme de la différence de deux carrés. Alors ce nombre est composé et deux de ses facteurs sont immédiatement connus.

MÉTHODE
Approche Voir Identité remarquable Formulation Si N = a² – b² alors N = (a – b) (a + b)

Cas particuliers
Cas de b = 1 Dans ce cas la valeur de N devient: N = a² – 1 Les facteurs sont: a – 1 et a + 1 Exemples Cas de b = 2 Dans ce cas la valeur de N devient: N = a² – 4 Les facteurs sont: a – 2 et a + 2 Exemples Cas de b = 3 Dans ce cas la valeur de N devient: N = a² – 9 Les facteurs sont: a – 3 et a + 3 Exemples

Cas de b = a – 1

Dans ce cas la valeur de N devient:

N = (a – a + 1) (a + a – 1) = 2a – 1

N est un nombre impair

Réciproquement:

Un nombre impair 2a – 1 est égal à la différence de carrés de deux nombres consécutifs.

2a – 1 = a² – (a – 1)²

Voir Développement sur ce thème

Suite	Table des différences de carrés de 1 à 100 S'y retrouver
Voir	Addition – Glossaire Addition des carrés Connaître les carrés des nombres Machine des frères Carisan TABLES – Index
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Addition/P100a500/Factoris.htm