famille infinie de sommes de carrés doublées

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 22/09/2021 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Partitions
Débutants Addition	Variations sur les carrés				Glossaire Addition
INDEX PARTITION	Carrés	Chiffres répétés	Repdigits
	Produits	66 x 67 …	66 x 99 …	Factorisation
	Sommes	Somme double	A² + kB²	Factorisation – Algorithme
	Différences	Propriétés	Écart 1, 2, …	Trouver la dif. des carrés
	Autres	Table 1 à 100	Repdigits	Table des Repdigits
		Curiosités	Tableau synthèse	a² – b² = c² – d²
		Chiffres	Concaténation
	Sommaire de cette page >>> Sommes de deux carrés jusqu'à 200 >>> La magie s'explique >>> Histoire de doubles >>> Cousins par la somme des carrés >>> Famille infinie de doubles

Somme de deux CARRÉS

Page découverte et travaux pratiques.

Un nombre N somme de 2 carrés fait partie d'une famille infinie.

Tous les multiples sont aussi somme de 2 carrés.

13 = 2² + 3²

2 x 13 = 5² + 1²

4 x 13 = 6² + 4²

Quelles sont leurs relations ?

SOMMES de deux carrés jusqu'à 200

On forme le tableau des nombres somme de deux carrés: N = a² + b²

a de 1 à 10 en abscisse.

b de 1 à 10 en ordonnée.

10											200
9										162	181
8									128	145	164
7								98	113	130	149
6							72	85	100	117	136
5						50	61	74	89	106	125
4					32	41	52	65	80	97	116
3				18	25	34	45	58	73	90	109
2			8	13	20	29	40	53	68	85	104
1		2	5	10	17	26	37	50	65	82	101
0	0	1	4	9	16	25	36	49	64	81	100
b / a	0	1	2	3	4	5	6	7	8	9	10

Ils sont tous là, jusqu'à 10² + 10² = 200.

Sur fond jaune, tous ceux avec 5².

En vert-gras, on retrouve deux fois les nombres 25, 50, 100 et 85.

Il y a 1 + 2 + 3 =+ … + 11 = 11x12/2 = 66 sommes de deux carrés.
Et 66 – 4 = 62 sommes différences; soit 62 / 200 = 31%.

On constate que les nombres somme de deux carrés ne sont pas très nombreux. Pour couvrir tous les nombres, il faut sommer 4 carrés.

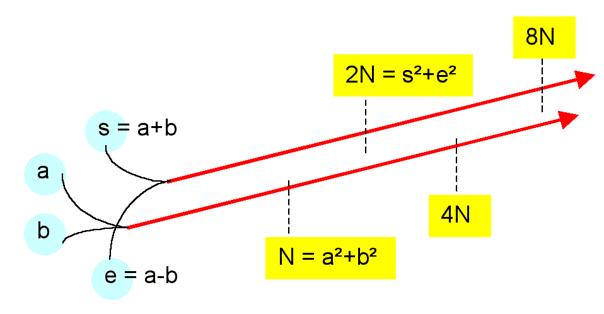
Observations sur les doubles

Partons de 1 et cherchons les doubles successifs: 2, 4, 8 …

Observons les valeurs de a et b

et de leur somme s = a² + b² et différence e = a² - b² .

10											200
9										162	181
8									128	145	164
7								98	113	130	149
6							72	85	100	117	136
5						50	61	74	89	106	125
4					32	41	52	65	80	97	116
3				18	25	34	45	58	73	90	109
2			8	13	20	29	40	53	68	85	104
1		2	5	10	17	26	37	50	65	82	101
0	0	1	4	9	16	25	36	49	64	81	100
a / b	0	1	2	3	4	5	6	7	8	9	10

N	a	b	s	e
1	1	0	1	1
2	1	1	2	0
4	2	0	2	2
8	2	2	4	0
16	4	0	4	4
32	4	4	8	0
64	8	0	8	8
128	8	8	16	0

Conclusion

Pour doubler la somme de deux carrés,

on calcule une nouvelle somme de carrés

en prenant la somme et la différence de a et b.

N = a² + b²

a' = s

b' = e

2N = a'² + b'²

2N = s² + e²

En pratique

4	3	N = 4² + 3²	= 25
a' = s = 7	b' = e = 1	2N = 7² + 1²	= 50
a" = 8	b" = 6	4N = 8² + 6²	= 100
a"' = 14	b"' = 2	8N = 14² + 2²	= 200

Essayons encore

Partons de 5 et cherchons les doubles successifs: 10, 20 …

10											200
9										162	181
8									128	145	164
7								98	113	130	149
6							72	85	100	117	136
5						50	61	74	89	106	125
4					32	41	52	65	80	97	116
3				18	25	34	45	58	73	90	109
2			8	13	20	29	40	53	68	85	104
1		2	5	10	17	26	37	50	65	82	101
0	0	1	4	9	16	25	36	49	64	81	100
a / b	0	1	2	3	4	5	6	7	8	9	10

N	a	b	s	e
5	2	1	3	1
10	3	1	4	2
20	4	2	6	2
40	6	2	8	4
80	8	4	12	4

Conclusion

On vérifie bien la même propriété.

LA MAGIE S'EXPLIQUE

La magie s'explique même très facilement pour un collégien.
Encore un coup des identités remarquables.

N	= a² + b²
2N	= 2a² + 2b²
	= a² + 2ab + b² + a² - 2ab + b²
	= (a+b)² + (a-b)²
2N	= s² + e²

Théorème

= a² + b²

= s² + e²

avec

s = a + b

e = a - b

Dés que l'on tient un nombre (N) somme de deux carrés, on en tient une infinité (2k.N) et nous avons aussi la manière de les construire: l'un est la somme (s) et l'autre est la différence (e).

Exemple: famille 4² + 1² = 17

a²

b²

a² + b²

somme 5

128

160

256

320

512

640

1024

1280

2048

2560

écart 3

192

128

384

256

768

512

1536

100

256

400

1024

1600

4096

6400

16384

25600

65536

102400

262144

409600

1048576

1638400

4194304

6553600

144

576

256

2304

1024

9216

4096

36864

16384

147456

65536

589824

262144

2359296

136

272

544

1088

2176

4352

8704

17408

34816

69632

139264

278528

557056

1114112

2228224

4456448

8912896

…

HISTOIRE DE DOUBLES

Observons les valeurs successives de a et b.
Elles sont doubles les unes des autres, une fois sur deux.

Exemple: famille 10² + 1² = 101

a	b	a²	b²	*a² + b²*
10	1	100	1	101
11	9	121	81	202

20	2	400	4	404
22	18	484	324	808
40	4	1600	16	1616
44	36	1936	1296	3232
80	8	6400	64	6464
88	72	7744	5184	12928

2k.a	2k.b			4k² (a² + b²)
2k.s	2k.e			4k² (s² + e²)

Explications

a			= a
	b		= b
s1 = a + b			= s
	e1 = a - b		= e
s2 = s1 + e1		= a + b + a - b	= 2a
	e2 = s1 - e1	= a + b - (a - b)	= 2b
s3 = s2 + e2		= 2a + 2b	= 2s
	e3 = s2 - e2	= 2a - 2b	= 2e

COUSINS PAR LA SOMME DES CARRÉS

Nous avons eu la surprise de détecter une famille infinie. Les spécimens trouvés semblent des frères-doubles une fois sur deux. On peut expliquer une fois encore.

*Nombres*		*Somme de leur carrés*
a	b			= a² + b²
2a	2b	4a²	+ 4 b²	= 4 (a² + b²)

Si on double les nombres de départ, on quadruple la somme de leur carré

Bon on retrouve notre résultat: 101 , 404 , 1616

Donc avec une somme de deux carrés, on engendre une famille infinie de quadruples.

En fait, le procédé permet de trouver une autre famille: celle ayant pour départ s = a + b et e = a – b.

*Nombres*		*Somme de leur carrés*
a	b		N	= a² + b²
e	s		2N	= s² +e²
2e	2s		4 (2N)	= 4 (s² + e²)

C'est également une famille infinie de quadruples qui s'intercale dans la précédente pour former, ensemble, une famille infinie de double.

FAMILLE INFINIE DE DOUBLES

Illustration des conclusions

La famille infinie de doubles
formée de deux familles de quadruples
(N, 4N, 16N … et 2N, 8N, 32N …) intercalées,
engendrées par a et b et,
leur somme s et leur différence e.