|
||||||||||||||||||||||||||||||||||||||||
![]()
|
CARRÉS MAGIQUES de B.Franklin d'ordres 4, 8 et 16 Le fameux carré magique d'ordre 8 de Benjamin Franklin a été publié en 1769 à Londres: Letters and papers on Philosophical
subjects by Benjamin Franklin. Il écrit de Philadelphie à Peter Collinson
à Londres. Il annonce un curiosité arithmétique (I now send you the
arithmetical curiosity …). Franklin se serait inspiré d'un livre sur
les carrés magiques écrit par Frenicle
de Bessy (1605-1675): Des Quarrez magiques. Les "carrés magiques" de Franklin
sont particuliers: dotés d'innombrables propriétés au prix du remplacement
des diagonales des semi-diagonales. |
Benjamin
Franklin is on $100 dollar bill.

Le billet de 100 dollars est la plus
grosse coupure américaine. Franklin y figure sans avoir été Président.
|
|
||
|
I had amused myself in
making these kind of magic squares, and, at length had acquired such a knack
at it, that I could fill the cells of any magic square of reasonable size
with a series of numbers as fast as I could write them, disposed in such
manner that the sums of every row, horizontal, perpendicular or diagonal,
should be equal; but not being satisfied with these, which I looked on as
common and easy things, I had imposed on myself more difficult tasks, and succeeded
in making other magic squares with a variety of properties, and much more
curious. |
Je me suis amusé à réaliser cette sorte de carrés magiques, et, à la
longue, j'ai acquis un tel savoir-faire que je pouvais remplir les cellules
de n'importe quel carré magique de taille raisonnable avec une série de
nombres aussi rapidement que je pouvais les écrire, rangés de telle sorte que
la somme des rangées, horizontales, perpendiculaires ou diagonales soit
constante; mais, n'en étant pas satisfait, car je les considérais comme
choses communes et faciles, je me suis imposé des tâches plus difficiles et
j'ai réussi à faire d'autres carrés magiques possédant diverses propriétés,
et encore plus de singularités. |
|
Voir Anglais
/ Biographie de Franklin
![]()
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Présentation Le carré est un carré magique
inhabituel
Notez la disposition des nombres en
zigzags, en serpentin
D'autres
présentations existent, mais ce ne sont que des variantes par premutations. Sommes particulières
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Astuce
|
Sur
tableur, facilitez-vous la vie
en copiant quatre fois le carré magique. Vous obtenez un carré de 8x8 (illustration) simulant les enroulements cylindriques. Une
autre manière de voir, utilisée comme image par Franklin: copiez quatre fois
le carré magique. Avec un carton, ajourez la forme désirée (ici un carré
4x4). Vérifiez que vous obtenez bien la même somme dans la fenêtre en
déplaçant le carton. |
|
– La magie du carré de Franklin |
|
||
|
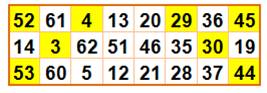
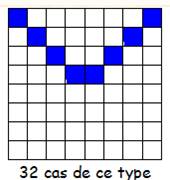
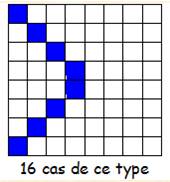
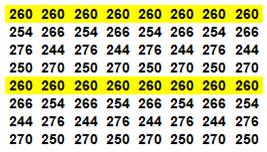
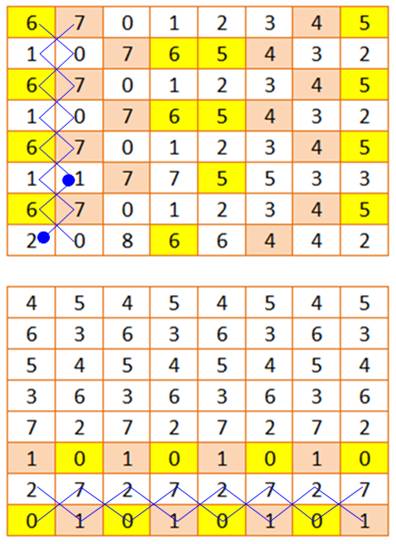
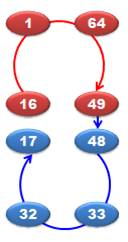
Le carré de Franklin comporte 96
telles semi-pandiagonales magiques (ou diagonales pliées ou bent row en
anglais). Type de somme en bleu et toutes les sommes par translation de cette
figure en jaune. |
|||
|
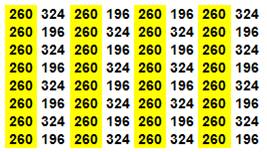
Type 1 52
+ 3 + 5 + 54 + 43 + 28 + 30 + 45 = 260 4 + 51 + 61 + 38 + 27 + 44 + 14 + 61 = 260 20
+ … 36
+ … Cela 8 fois par translation d'un cran vers le bas. |
|
|
|
|
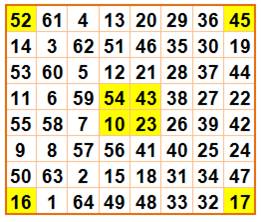
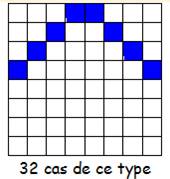
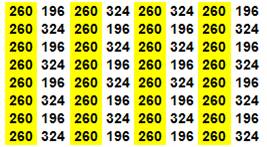
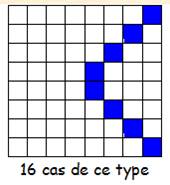
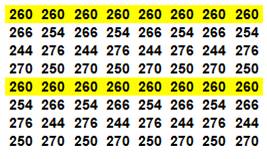
Type 2 11
+ 60 + 62 + 13 + 20 + 35 + 37 + 22 = 260 59
+ … 43
+ … 27
+ … Cela 8 fois par translation d'un cran vers
le bas. |
|
|
|
|
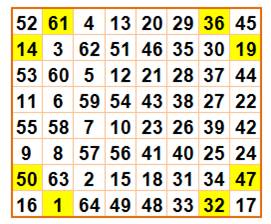
Type 3 52
+ 3 + 5 + 54 + 10 + 57 + 63 + 16 = 260 55
+ 8 +
2 + 49 + 13 + 62 + 60 + 11 = 260 Cela 8 fois par translation d'un cran vers
la droite. |
|
|
|
|
Type 4 13
+ 62 + 60 + 11 + 55 + 8 + 2 + 49 = 260 10
+ 57 + 63 + 16 + 53 + 3 + 5 + 54 = 260 Cela 8 fois par translation d'un cran vers
la gauche. |
|
|
|
|
|
||
|
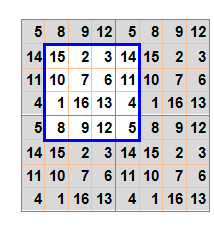
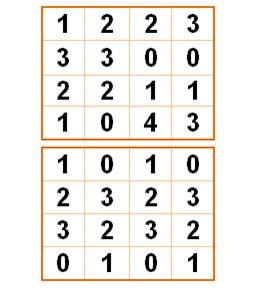
Le carré
est décomposé en deux carrés:
Cette
présentation donne le "spectre" du carré et permet de reconnaitre
la méthode de construction. Les deux
carrés forment bien un carré gréco-latin: aucun
couple de deux nombres ne se répète. Il a cependant une particularité:
On
remarque immédiatement la disposition en serpentin vertical pour le premier
et horizontal pour le second. Cependant, comme pour tout carré magique
d'ordre pair, il y a des exceptions (exemples avec les ronds bleus). |
|
|
|
|
||
|
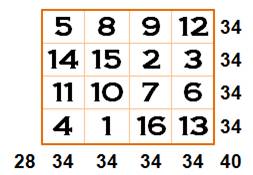
Le carré
semi-panmagique d'ordre 4 présente les mêmes propriétés que son grand frère
d'ordre 8.
et aussi toute suite de 4
nombres (avec enroulement comme 8 + 9 + 12 + 5 = 34
et aussi toute suite de 4
nombres (avec enroulement comme 14 + 11 + 4 + 5 = 34
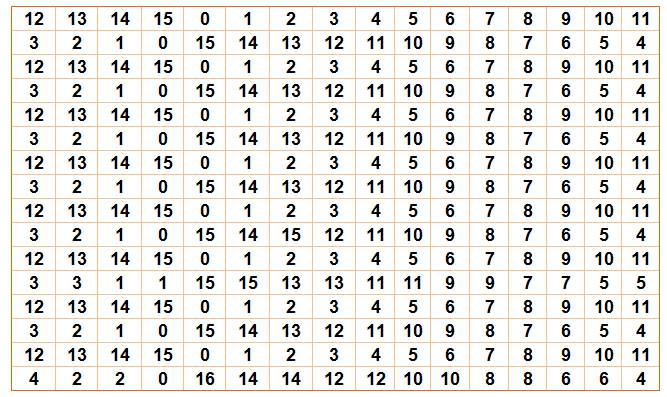
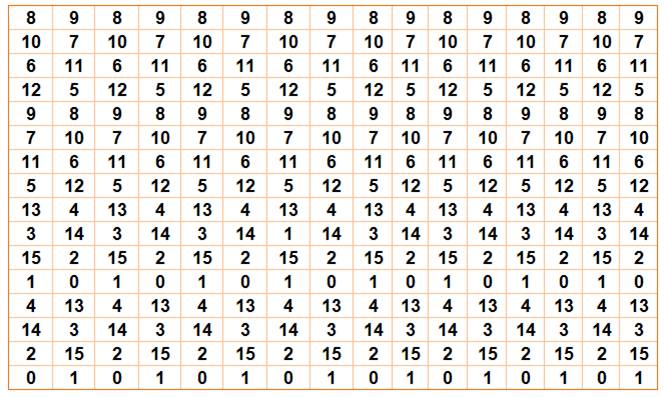
Sa décomposition
en deux matrices quotients et restes montre sa structure interne et le
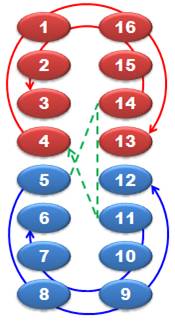
principe de sa construction. Notez la présence du 4 dans la matrice quotient. Le graphe
rouge et bleu montre la succession des nombres dans le carré magique. L'ordre
de prise en compte des lignes est montré en vert. Notez la belle symétrie. Les
autres carrés de Franklin présentent exactement la même allure de graphe. Note: contrairement à
la structure gréco-latine, cette représentation en serpentin ne souffre
d'aucune exception. Voir Carrés
gréco-latins à échelle alternée |
Carré 4x4 de Franklin
Matrices quotients et
restes
Graphe montrant la
succession des nombres Carré 4x4
complet et carré 8x8, ligne du bas
|
|
Voir Carré d'ordre
4
|
|
|
|
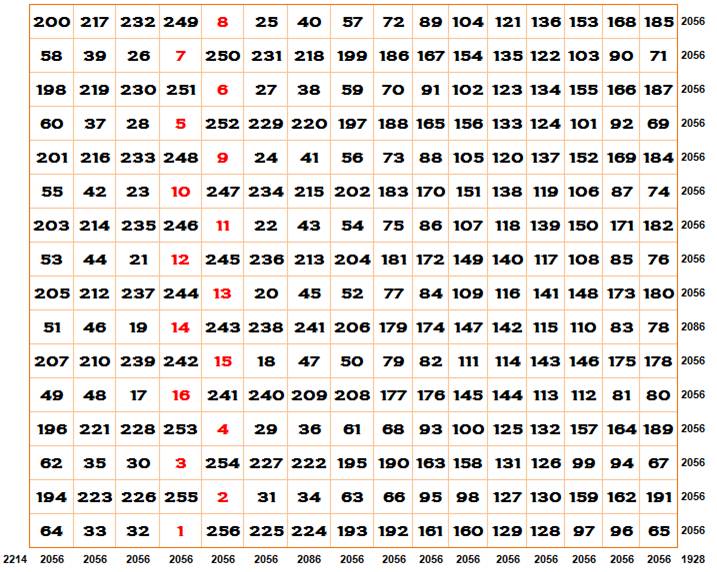
Carré semi-panmagique
16 x 16 de Benjamin Franklin
Toutes
les propriétés du carré de B. Franklin Tous les
carrés 4x4 somment également en 2056. Il y en a 16 x 16. Tous les
carrés 2x2 somment 514 = 2056 / 4. Il y en a 16 x 16. Je laisse le
soin aux lecteurs de trouver de nombreuses autres configurations magiques. Structure quotients et
restes
|
|
![]()
|
|
|
|
Homme politique, publiciste et
physicien américain Né à Boston. Quinzième enfant et
dernier d'un marchand de chandelles et de savon. Encouragé à devenir pasteur, se
retrouve imprimeur. Chercheur, passionné des phénomènes
électriques. Il a été reçu par la Société Royale de Londres et par l'Académie
des sciences de Paris. Inventeur de génie: le paratonnerre
en 1752, l'harmonica de verre, les lentilles bifocales, etc. Passionné de jeux, notamment les carrés magiques. Contribue à la vie publique en
Amérique: première bibliothèques publiques, premiers hôpitaux, premières
brigades de pompiers volontaires; actions pour l'abolition de l'esclavage En 1774, il devient député du
premier Congrès des États-Unis. En 1176, B. Franklin, Thomas
Jefferson, John Adams et deux autres personnes (Comité des Cinq) rédigent le
manifeste de la Déclaration d'Indépendance des États-Unis. Il est missionné par George
Washington, chef des insurgés et futur président, pour obtenir l'appui des
pays européens hostiles à l'Angleterre, dont la France. En 1776 (70 ans), il arrive en
France et attire la sympathie notamment du fait de sa bonhommie et de son
look: habit de velours et toque de trappeur. Il arrive à convaincre bon
nombre de volontaires dont le marquis de La Fayette. En 1778, traité d'alliance avec
Louis XVI. La participation française à la guerre d'indépendance des
États-Unis fut décisive. B. Franklin passe huit ans en France
et à sa mort en 1790, la France décrète un deuil national de trois jours. |
|
|
L'odeur
du poisson et des visiteurs reste trois
jours. B. Franklin – Poor Richard Almanach. |
Voir Pensées & humour
![]()
|
Suite |
|
|
Voir |
|
|
Diconombre |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/CMFrankl.htm |
![]()