|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Tableau pour TESTS et QCM
répétitifs
Une batterie de tests avec
réponses à choix multiples. Les réponses sont choisies
dans une liste et peuvent se retrouver plusieurs fois dans la suite des tests,
mais jamais deux fois dans un test particulier. Le problème peut être généralisé: comment remplir
un tableau (une matrice)
avec un minimum de nombres tels que chaque ligne est différente des autres et
chaque nombre n'est pas répété plus de tant de fois. On côtoie les notions de carrés
latins et de principe
des tiroirs. |
Anglais:
Multi choice questions (MCQ)
|
|
|||
|
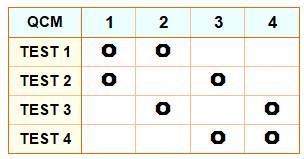
Avec ce
QCM, on propose quatre tests, chacun avec deux réponses proposées parmi un
jeu complet de quatre réponses (deux réponses sur chaque ligne). Dans le
jeu complet des quatre réponses, chacune ne peut pas être utilisée plus de
deux fois pour l'ensemble des tests (max: 2 fois en colonne). |
Les tests (ou questions) comportent chacun deux réponses possibles parmi un jeu complet de
quatre réponses. |
||
|
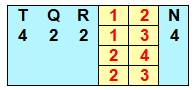
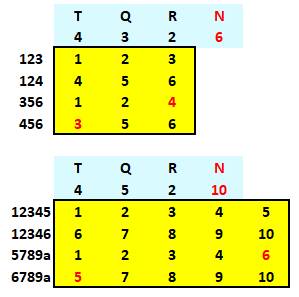
On résume avec un tableau (jaune) de 4 lignes (T
= 4) et 2 colonnes (Q = 2). On note le taux admis de répétitions: R = 2 et la
quantité de réponses (N = 4) dans le jeu complet des réponses. |
|
||
|
|
||||||||||||||||||||||||||
|
Problème On veut
réaliser T tests comportant Q questions. Chaque réponse
peut être répétée R fois, mais chaque test est différent des autres. Combien
de réponses faut-il, au minimum ? Formulation mathématique Réaliser
une matrice T x Q avec le minimum N de nombres successifs, répétés au
plus R fois. Les
nombres sont distincts sur les lignes et peuvent être répétés sur les
colonnes. Les
lignes (et donc les colonnes) sont toutes différentes. |
Notations
Exemple Trois tests de
quatre réponses:
Pour 12 cellules, il faut 6 nombres
répétés deux fois, en les disposant correctement. |
|||||||||||||||||||||||||
|
|
||
|
Après divers essais avec papier-crayon, tableur ou programmes,
on trouve les résultats qui suivent. Explications dans les chapitres
suivants. |
||
|
Règles 1.
R ne dépasse par T (sinon la même réponse serait répétée dans un test;
principe des tiroirs); 2.
N minimum: N = T.Q / R si cette
valeur entière, ou son arrondi supérieur si fractionnaire; 3.
Si N est inférieur ou égal à Q, alors N vaut Q + 1 (sinon pas assez de
chiffres sur une ligne et éviter la répétition sur la ligne suivante); et 4.
Si N = QR, un phénomène cyclique s'installe. |
Bilan sur la valeur de N N = plafond de T.Q / R, sauf si ce nombre est inférieur ou égal à Q, auquel
cas N = Q + 1. Bilan sur la construction du tableau La construction est toujours possible par simple distribution
des nombre de 1 à N répétés autant que nécessaire pour remplir les lignes, sauf si N =
QR, auquel cas, on choisit une permutation différente à chacun des cycles. |
|
![]()
|
Après
avoir découvert comment organiser les tests, on poursuit le chemin en butant sur
quelques embûches: existence d'exceptions ou formation de cycles difficiles à
éliminer. Le
principe général consiste à faire "couler" une suite continue de
nombres dans les cellules du tableau. Dans une majorité des cas, les
conditions requises sont remplies. La
formation de cycle donne du fil à retordre et nécessite de faire appel aux
permutations. |
|
CAS
(3, 3, 2) – Découverte et méthode |
|
|||||||||||||||||||||||
|
Les six solutions Pour 3
tests de 3 réponses répétées 2 fois, il faut un jeu complet de 5 réponses (N
= 5). Pour ce tableau de 9 cellules, il faut un minimum
de 4 nombres répétés deux fois et un
nombre supplémentaire (le 5, unique). Soit 4 x 2 + 1 = 9. Dans ce cas, on calcule: |
|
|||||||||||||||||||||||
|
Méthode de remplissage 1 Pour 9 cellules, on va donc jusqu'à 5, selon le
calcul précédent.
|
Première solution du tableau
|
|||||||||||||||||||||||
|
Méthode de remplissage 2 Pour 9 cellules, on va toujours jusqu'à 5.
|
Troisième solution du tableau
|
|||||||||||||||||||||||
|
CAS
(3, 4, 2) – Remplissage normal |
|
|||||||||||||||||||||||||||||
|
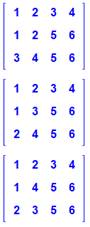
Les quinze solutions Pour 3
tests de 4 réponses répétées 2 fois, il faut un jeu complet de 6 réponses (N
= 6). Pour 12 cellules, il faut 6 nombres répétés deux
fois. Dans ce cas, on a: |
|
|||||||||||||||||||||||||||||
|
Méthode de remplissage 2 Cette méthode de remplissage marche pour ce cas. Le tableau commuté et ordonné (en bleu), pour
retrouver une des 15 solutions ci-dessus. N = 6. |
|
|||||||||||||||||||||||||||||
|
CAS
(3, 5, 2) et (3, 5, 3) – Exception |
|
||||||||||||||||||||||||||||||||||
|
Cas (3, 5, 2) Pour 15 cellules et 2 répétitions, il faut 7
nombres répétés deux fois et un complémentaire. N = 7. Remplissage normal. Bien ! |
|
||||||||||||||||||||||||||||||||||
|
Cas (3, 5, 3) Selon la formule, il faut 3x5/3 = 5 nombres répétés
trois fois. Problème, cinq nombres sont juste suffisant pour
remplir une ligne. Il en faut un autre pour différencier la deuxième ligne. Si N calculé est inférieur ou égal à Q, alors: N = Q + 1 |
Alors que 5 nombres seraient suffisants, ici on
doit ajouter un nombre. Ils sont répétés: 3, 3, 3, 2, 2, 2 => total 15. |
||||||||||||||||||||||||||||||||||
|
CAS
(4, 3, 2) et (4, 5, 2) – Cycle |
|
|
|
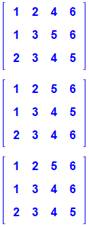
Dans ces deux cas, le remplissage standard se heurte
à un phénomène de cycle: les deux premières lignes se répètent sur les deux
lignes suivantes. On aurait tendance à vouloir ajouter un nombre de
plus pour briser le cycle. Or, il existe des solutions en conservant la
quantité de nombres calculée. En rouge, les solutions proposées en croisant
deux nombres. Malheureusement, cet artifice ne marche pas à tous les coups.
Il faut recourir à des choix plus subtils de permutations,
surtout si la batterie de tests comporte plusieurs cycles. |
À droite, les combinaisons ordonnées en ordre
croissant sur les lignes, puis sur les colonnes. |
|
![]()
|
|
||
|
Pour
procéder à l'analyse de ce problème, le mieux pour débuter est de travailler
avec le tableur, puis vient rapidement l'envie de tester avec un programme. La
programmation n'est pas simple sans être très compliquée. J'ai adopté une démarche
avec remplissage
de matrices et deux stratégies: |
||
|
Recherche systématique On calcule la valeur de N, la quantité de nombres
à répartir dans la matrice. On énumère les combinaisons de Q nombres parmi
ces N. On sélectionne T de ces combinaisons qui
deviennent les lignes du tableau. Les lignes sont alors systématiquement différentes;
reste à vérifier que les nombres ne sont pas répétés plus de R fois. |
Construction du tableau On calcule la valeur de N. On forme une suite de N nombres que l'on écoule
cycliquement dans la matrice (lignes, puis colonnes) Cette suite est une concaténation de R fois des permutations
des nombres de 1 à n. On teste si les lignes sont bien différentes,
sinon on choisit d'autres permutations. |
|
|
Le programme est simple à écrire pour un cas
donné. Il est plus délicat de le généraliser à tout type de cas. Avantage: toutes les possibilités pour un cas
donné sont énoncées. Inconvénient: le temps de calcul devient vite
important. |
Principale complexité, sélectionner les
permutations surtout en cas de nombreux cycles. Avantage: temps de calcul minimisé. Inconvénient: ne donne que le cas prévu par cette
sorte de construction. |
|
Voir Programmation – Index
|
|
||
|
etc. |
Recherche systématique Initialisation et appel du logiciel combinatoire. Indication des paramètres (T, Q, R). Liste des nombres de 1 à N avec N valant 6.
Combinaisons de 4 parmi les éléments de L. Quantité de combinaisons en qLL. Trois boucles pour trois lignes du tableau qui
balaie toutes les combinaisons trois par trois. Avec ces trois combinaisons pour lignes,
formation de la matrice A. Reste à vérifier que la matrice est valide en
comptant la quantité de chacun des six chiffres (avec C). Boucle de balayage des lignes de 1 à 3 (T) et des
colonnes de 1 à 4 (Q) et pour chaque valeur de nombre trouvée, incrémentation
du compteur correspondant dans C. On vérifie alors que la quantité de chacun des
nombres (chacune des positions dans C) est inferieur à 2 (R). Si une valeur dépasse 2, le témoin test, positionné au préalable à 1, passe
à 0. On compte la quantité de solutions valides avec
le compteur kt. On a demandé l'impression de la liste des combinaisons,
à titre indicatif. Les quinze solutions sont imprimées à la suite
les unes des autres. |
|
|
As one of the tools for
summative assessment, multiple choice questions (MCQs) offer many advantages.
They can be marked reliably and
quickly, making them cost and time efficient for large groups, and they can
be used to cover a broad range of content within a short test. En
tant qu'un des outils de l'évaluation sommative, les questions à
choix multiples (QCM) offrent de nombreux avantages. Ils
peuvent être commercialisés de manière fiable et rapide, ce qui les rend
rentables et économiques pour les grands groupes, et ils peuvent être
utilisés pour couvrir une large gamme de contenu à l'occasion d'un test
court. |
Voir
Anglais pour le bac et pour les affaires
Merci à Daniel Diaz pour son idée et sa
contribution
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/aaaMaths/TestQCM.htm
|
![]()