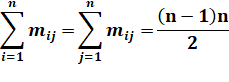|
||||||||||||||||||||||||||||||||
![]()
|
Mathématiques des Carrés Magiques Les carrés latins (CL)
Il est normalisé ou standard ou réduit si ces nombres
de 1 à n sont en première ligne et première colonne. Tous les autres carrés
latins du même ordre s'en déduisent par symétries et permutations. Le carré
latin est semi-magique: même somme sur les
lignes et sur les colonnes. Le Sudoku est une variété sophistiquée de
carré latin. |
Voir
Introduction aux carrés latins et amusements
|
|
||
|
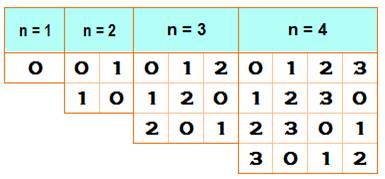
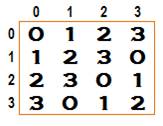
Existence Il existe au moins un carré
latin pour tout entier n comme le montre l'illustration. En maths, on remplit
habituellement avec les nombres de 0 à n–1. |
|
|
|
Formulation de la définition Elle exprime que la somme,
sur chacune des lignes comme sur chacune des colonnes, vaut la même somme (somme
des nombres de 0 à n–1. |
|
|
|
Représentation par triplets Chaque
cellule du carré est caractérisé par un triplet: (l, c, s) Ligne, colonne, symbole. Sur l'illustration, le 0 e haut à gauche du carré latin est représenté
par le triplet (1, 1, 0) Notation
utile pour le traitement informatique.
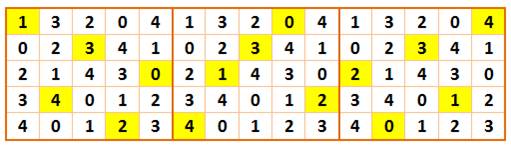
Présentation sous forme matricielle
ou en ligne. Les lignes et colonnes sont alors numérotées à partr de 0. De
nouveaux carrés latins peuvent être obtenus, par exemple, en remplaçant
(l,c,s) par (s,c,l). Voir le tableau
central, remis en ordre en bas. Ce type
d'opération crée six carrés latins dits conjugués. |
|
|
|
Isotope et normalisation Tout
carré latin peut être rendu
standard par permutation linéaire. |
Un carré
latin dont les lignes et/ou colonnes sont permutées est un isotope de l'original. Un carré
latin dont la première ligne et la première colonne contiennent les nombres
de 1 à n dans l'ordre est dit normalisé ou
standard. |
|
Diagonal ou antidiagonal Le
carré latin doit être diagonal pour engendrer un carré
magique. |
Le carré
est diagonal si ses deux diagonales
principales contiennent les nombres de 0 à n–1, une seule fois. Il est antidiagonal si certains nombres sont répétés |
|
Cellules conjuguées et Carré symétrique |
Deux
cellules symétriques par rapport au centre du carré sont dites conjuguées. Si toutes
les cellules conjuguées sont identiques, le carré est symétrique. |
|
Carré latin avec sous-carrés Notion
utilisées pour la recherche sur les carrés latins. La notion de rectangle
latin (carré latin tronqué) est également utilisée. |
Carré latin
n × n partagé en k² sous-carrés k × k, tels que chacun contienne les nombres de 0 à n–1. Le Sudoku est un tel carré. |
|
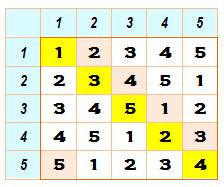
Un type de formulation pour l'ordre impair
Tels que définis, ces carrés latins
sont d'une race particulière. Ils n'ont pas de correspondants orthogonaux. Le
chapitre suivant explique la méthode qui en permet la démonstration. |
Règles 1 et 2 => en jaune Règles 3 et 4 => en rose Règle 5 => en blanc |
Voir Exemple de transversales
pour le carré 6x6
|
|
||
|
La formulation la plus simple
Addition des indices de
lignes et de colonnes en modulo n. Voir Table d'addition |
|
|
|
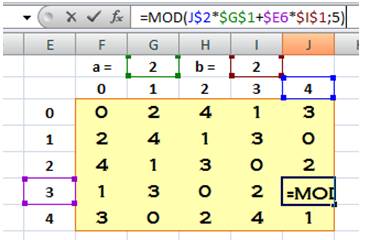
La même formule généralisée Carré
latin d'ordre n quelconque avec deux semence a et b, nombres compris entre 0
et n – 1. Les calculs sont exécutés modulo n. Le
carré est alors latin pour tout n à condition que a et b, compris entre 1 et
(n–1) soient premiers avec n.
Programmation sur tableur pour n = 5, a = 2 et b = 2 |
||
|
|
|||
|
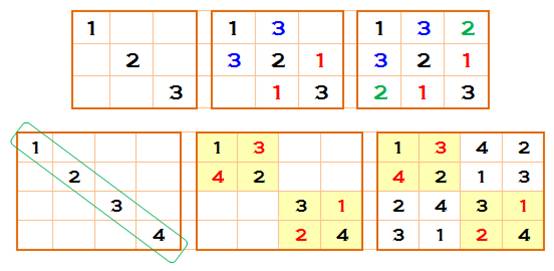
Carré 3x3 Un essai montre que c'est
impossible. La seconde diagonale est en 2. Carré 4x4 La diagonale est remplie
(vert). Une idée consiste à placer les deux nombres du haut de la diagonale en
bas et réciproquement (en rouge). La suite s'impose comme pour
le Sudoku. |
Notez que le carré latin est partagé en quatre quarts, chacun
contenant les quatre nombres, comme au Sudoku 4x4 pour kids. |
||
|
Cas n quelconque Méthode classique vue
ci-dessus à condition que (a + b) et (a – b) soient premiers avec n. Avec a et b compris entre 1 et n–1, et a, b, a+b et a-b premiers avec n, alors le carré latin est diagonal. Exemple Avec n = 5, a = 2 et b = 1. a + b = 3 et a – b = 1 qui
sont bien premiers avec 5. D'ailleurs, il est immédiat
d'en déduire: Avec a = 2 et b = 1, si n est impair
et non divisible par 3, alors le carré latin est diagonal. Avec n = 6, impossible de réunir ces conditions. Théorème Le transposé d'un carré latin ainsi produit, lui est orthogonal Transposé =
symétrique par rapport à une diagonale (comme plié le long de la diagonale). |
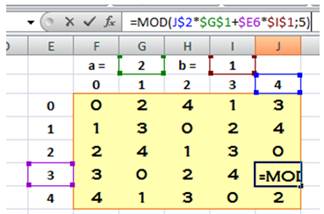
Création sur tableur
Copie du tableur
avec mise en évidence de la formule utilisée: =MOD(J$2*$G$1+$E6*$I$1;5) Rappel: sur tableur, le symbole $ sert à fixer
la ligne, la colonne ou les deux. |
||
Voir
Construction de carrés magiques à partir de cette
méthode
|
|
||
|
Diagonale et transversale Notion utilisée pour trouver
les carrés orthogonaux à un carré latin donné. Un carré latin possède un jumeau orthogonal
si et seulement s'il peut être décomposé en transversales disjointes. Le dénombrement des transversales d'un carré
latin est un objet de recherche mettant en œuvre des outils mathématiques
avancés. Toutes les transversales
réunies forment l'ensemble des permutations figurées
(ou permutations de Lucas) des nombres de 1 à n. |
Une transversale d'un carré latin est un ensemble de
n entrées distinctes chacune
représentative d'une ligne et d'une colonne.
Une diagonale est une "transversale" comprenant
des valeurs même répétées (sorte de diagonale en "vrac"). |
|
|
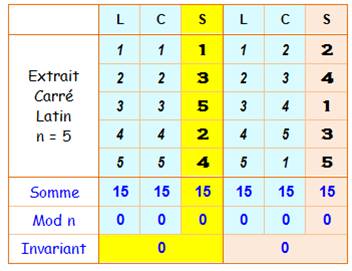
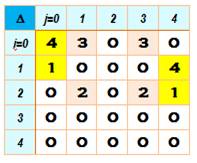
Le concept de transversale, Il s'agit d'une idée récente
(2005) pour tenter de mathématiser la recherche de carrés latins, notamment
l'identification d'un carré jumeau orthogonal (orthogonal mate). Sur ce carré latin d'ordre 5, deux transversales
sont identifiées (couleurs). Les numéros des lignes (L) et des colonnes (C)
sont marquées. Ces triplets (L, C et S, la valeur en L et C)
sont reportés dans le tableau du dessous pour chacune des deux transversales. On appelle Pour toute transversale d'un carré latin d'ordre impair n la somme des deltas modulo n est nulle. On vérifie que pour l'ordre pair: Pour toute transversale d'un carré latin d'ordre pair n la somme des deltas modulo n est égale à n/2.
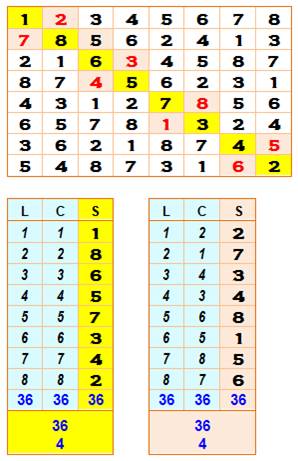
Les deux transversales en exemple sont
identifiées par les couleurs. Ce carré
latin comporte évidemment huit transversales. Les deux tableaux du bas montrent le calcul pour
chacune des deux transversales choisies. Si la somme des deltas un a un donne des valeurs
diverses y compris négatives, par contre en faisant la somme directement sur
les lignes, les colonnes et les valeurs, il est naturel de retrouver sur
chacune la somme des nombres de
1 à n. Soit: n(n+1)/2 = 4 x 9 = 36. La constante est alors (36 + 36 – 36) mod 8 = 36
mod 8 = 4 |
Un carré latin d'ordre 5
Calcul des invariants pour deux transversales
Carré latin d'ordre pair et calcul des invariants
|
|
Anglais:
transversal / disjoints transversals
|
Applications La littérature nomme ce type
de calcul: la méthode Delta Lemma. Elle permet la mise en œuvre de
démonstration sur l'existence de transversales et donc de l'existence de
carré latin orthogonaux. Euler utilisa cette méthode
pour démontrer que la table
d'addition n'a pas de transversales (1782). Cette méthode a permis de prouver que: Pour un ordre n supérieur à 3, il existe au moins un carré latin qui
n'a pas de jumeau orthogonal. Connu par Euler pour l'ordre pair et prouvé en
1944 par Mann pour n = 4k + 1. Le cas
n = 4k + 3 a résisté jusqu'à l'utilisation de la méthode delta (Evans –
2006). De très nombreuses lois ont
été découvertes ou redécouvertes en utilisant cet outil. |
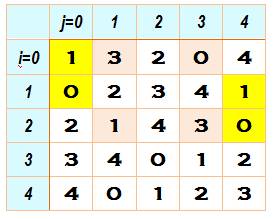
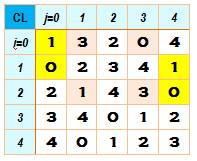
Dans le carré latin ci-dessus, la cellule
(1,0,0) conduit à delta = - 1 soit 4 mod 5. Le tableau de droite donne toutes
les valeurs de delta. Prenons la cellule (0, 1) et cherchons une transversale (solution
ci-dessous).
Non seulement c'est un peu plus facile pour l'exploration, mais,
surtout, il possible d'y tenir des raisonnements logiques permettant de
puissantes déductions. |
|
Les seules transversales du carré latin montré ci-dessus
Aucune transversales pour la cellule (1,0), comme pour
d'autres. Ces transversals ne sont pas disjointes: elles ont toutes
le 3 en commun. Notez que sans aide particulière, le travail de recherche
de ces transversales vaut bien un bon Sudoku. Autres connaissances: Conjecture: tout carré latin d'ordre impair possède
au moins une transversale. On sait qu'elle est vraie
jusqu'à n = 9. Théorème: tout carré latin d'ordre pair possède
une quantité paire de transversales. Démontré par Balasubramanian |
|
|
Sous leur aspect anodin, jeu d'arrangement pour école
primaire, les carrés latins sont un sujet d'études des mathématiques
avancées, et cela, du fait de leurs nombreuses applications:
La théorie mathématique se prolonge en considérant les
carrés munis des numéros de ligne et de colonnes (tables
de Cayley) comme une loi de composition
interne qui a les propriétés d'un quasigroupe. En tant carrés latins, les mathématiciens recherchent:
|
Codes
auto-correcteurs d'erreurs
|
Une idée pour imaginer comment cela fonctionne: Les grilles du Sudoku peuvent
avoir une solution unique si on dispose de 17 indices.
Si une grille à 81 (9×9) cases peut être résolue avec uniquement 17 indices présents, cela
signifie que ces indices permettent la restitution de l'ensemble en cas de
données manquantes ou incorrectes. Ce principe s'applique au transfert moderne de
données ou des objets similaires aux carrés latins sont utilisés comme outils
de correction d'erreurs. |
![]()
|
|
||
|
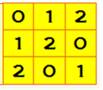
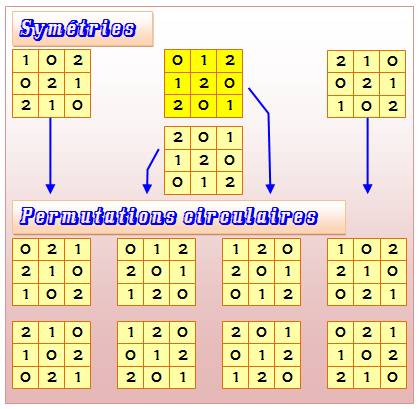
Les
carrés latins d'ordre 3 sont 12, mais tous se déduisent du carré normalisé
par symétries et permutations. Le carré latin normalisé est marqué en jaune
intense (1ère ligne et 1ère colonne en 0, 1 et 2). Son voisin de droite est son symétrique par
miroir vertical; son voisin en bas est son symétrique horizontal Son voisin de gauche est son symétrique par la
diagonale montante; son symétrique par la diagonale descendante est lui-même. Chacun engendrent deux nouveaux carrés par
permutations circulaires. Notez que chacun peut être obtenu par une
permutation horizontale ou une permutation verticale. |
Les 12 carrés latins d'ordre 3 dont un seul est le représentant de
tous les autres. |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Dénombrement Seules la
première ligne et la première colonne sont en ordre. Les
autres peuvent être différentes. Il y a 4
carrés normalisés d'ordre 4, 56 d'ordre 5 …
Relation
Ex: Pour n = 5, n! (n-1)! = 2 880 et 56 x 161 280 Il n'existe pas de formule pour dénombrer les carrés
latins. En 1973, il a fallu presque cinq heures pour dénombrer les carrés
d'ordre 9 (Stanley Bammel et Jerome Rothstein). En 1948, A. Sade en était à
l'ordre 7. Certains outils mathématiques ont été utilisés,
sans succès
|
Les quatre carrés normalisés d'ordre 4.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Bilan
|
Il n'existe pas de
formule pour dénombrer les carrés latins. Tout au plus des bornes min et max.
|
![]()
|
Suite |
|
|
Voir |
|
|
|
|
|
Référence |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/CarreMag/aaaMaths/Latin.htm |
![]()