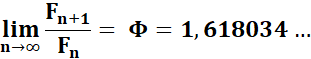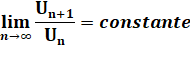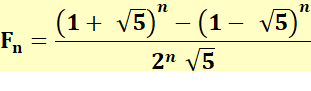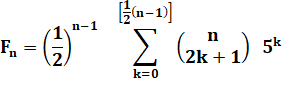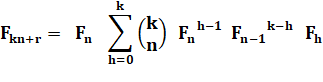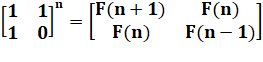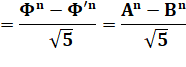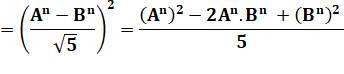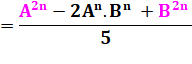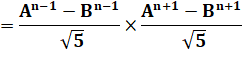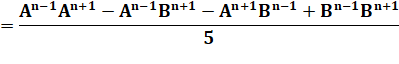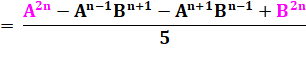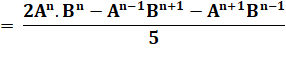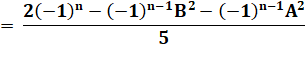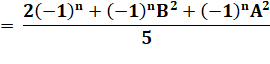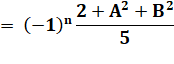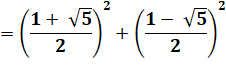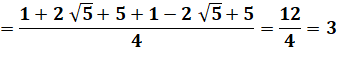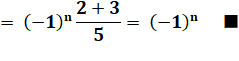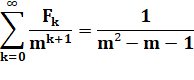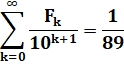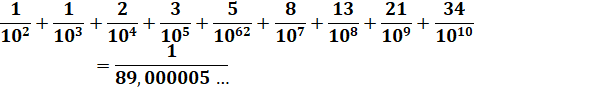|
|||||||||||||||||||||||||||||||
![]()
|
SUITE DE FIBONACCI Propriétés (2/2) dont Formule de Binet Revue des
principales propriétés des nombres de Fibonacci. Notamment comment calculer
les grandes valeurs directement sans avoir à calculer tous les précédents. En
pratique pour calculer un nombre de Fibonacci de rang n:
|
|
|
||
|
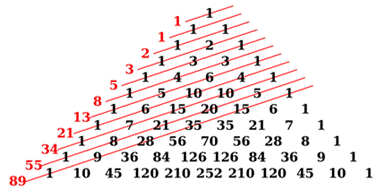
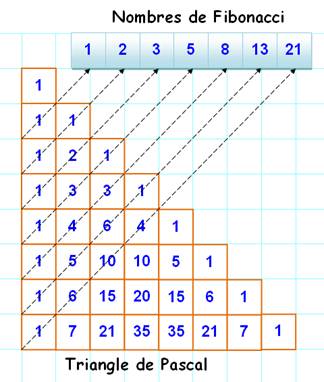
Dans
le triangle de Pascal, la somme des
"diagonales" forment la suite de Fibonacci. Présentation
classique du triangle Pascal
|
|
|
Voir Triangle de Pascal et Nombres de Fibonacci / Sommes en 2k
|
|
||||
|
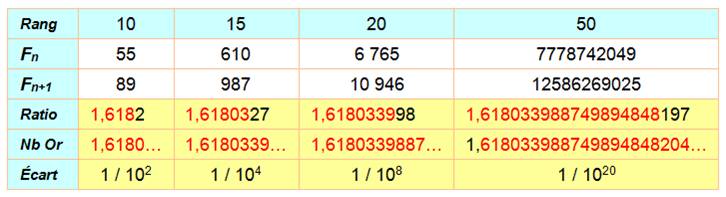
Le
rapport entre deux termes consécutifs tend vers le nombre d'or. |
|
|||
|
La
suite des nombres de Fibonacci est la seule suite
ayant les deux propriétés:
|
||||
Compléments en Nombre d'Or
|
|
||
|
Trois nombres de
Fibonacci consécutifs sont premier
entre eux par paires. Explication On sait que, par définition, Fn+1 = Fn + Fn–1 Si de divise deux des nombres, il divise le troisième. Par induction on remonte jusqu'à F1 = 1 qui n'est divisible
que par 1. |
(Fn-1, Fn) = (Fn-1, Fn+1) =
(Fn, Fn+1) = 1 Exemple F8 = 21 = 3 x 7 F9 = 34 = 2 x 17 F10 = 55 = 5 x 11 Aucun facteur en commun |
|
|
Le PGCD de deux nombres de Fibonacci est égal
au Fibonacci d'indice égal à ce PGCD. |
(Fn, Fm) = F(n,
m) Exemple F12 = 144 et
F18 = 2 584 PGCD(144, 2 584) = 8 PGCD(12, 18) = 6 F6 = 8 |
|
|
2 |
F3k
|
2, 8, 34, 144 … |
|
3 |
F4k |
3, 21, 144, 987 … |
|
4 |
F6k |
8, 144, 2 584, 46 368 … |
|
5 |
F5k |
5, 55, 610, 6 765 … |
|
6, 9 et 12 |
F12k |
144, 46,368, 14 930 352 … |
|
7 |
F8k |
21, 987, 46 368, 2 178 309 … |
|
10 et 61 |
F15k |
610, 832 040, 1 134 903 170 … |
|
11 |
F10k |
21, 987, 46 368, 2 178 309 … |
|
13 |
F7k |
13, 377, 10 946, 317 811… |
|
15 |
F20k |
6 765, 102 334 155 … |
|
17 |
F9k |
34, 2 584, 196 418, 14 930 352… |
|
29 |
F14k |
377, 317 811, 267 914 296 … |
|
Propriété exploitée Si m | n alors Fm | Fn |
Exemples 3
Si
3 15 | n alors n = 15k Si 15 | n alors F15 | Fn
soit 610 | F15k |
|
Voir Divisibilité des Fibonacci par 11 / Divisibilité
par n
|
|
||
|
|
|
|
Voir La formule de
Binet – Développements
|
|
|||||
|
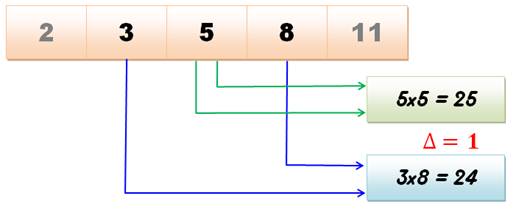
Propriété de l'expression E Le carré d'un nombre de Fibonacci est égal au
produit de ses deux voisins à 1 près. |
E
= Fn–1 . Fn+1 – Fn2 = (–1)n
Expression matricielle**
|
||||
|
Illustration
Démonstration Nous
noterons A et B le nombre d'or et son inverse en négatif. Souvenons-nous que leur produit est égal à –1. |
|||||
|
Formule de Binet Avec notation
facilitant la lecture |
FN |
|
|||
|
Carré Rappel: |
FN2 |
|
|||
|
Produit Rappel: produit de
puissances, on ajoute les indices. >>> |
Fn
– 1 . Fn +1 |
|
|||
|
Expression demandée |
E |
|
|||
|
Produit de AB |
A.B
An.Bn |
= – 1 = (A.B)n
= (– 1)n |
|||
|
Produits mixtes |
An-1.
Bn+1 An+1.
Bn-1 |
= (-1)n-1
B² = (-1)n-1
A2 |
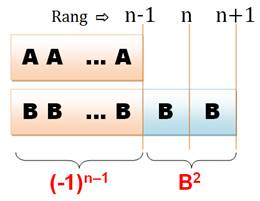
Explication
|
||
|
Les produits deux à deux de A et B jusqu'à n – 1 donne (–1); les deux B restants donnent le produit B². |
|||||
|
Remplaçons |
E |
|
|||
|
Somme des carrés |
A²
+ B² |
|
|||
|
Retour à E |
E
|
|
|||
|
|
|||
|
On peut
montrer que (m > 1): |
|
||
|
Avec |
Fn = 89 = m² – m – 1 => m =
10 |
||
|
En
remplaçant |
|
||
|
Calcul |
Avec 10 termes
Avec 20 termes 1 / 89,000000000000063930 |
||
Voir Nombre
89
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Iteration/FiboPro1.htm |
![]()