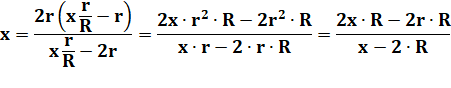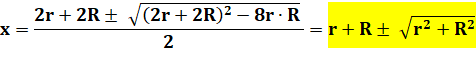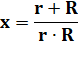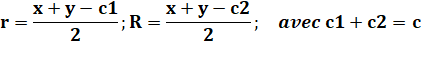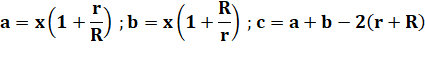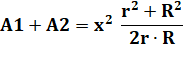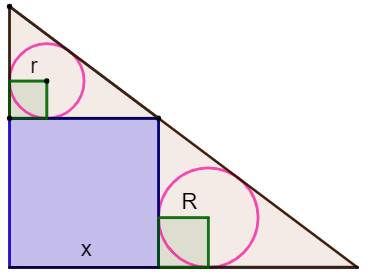
NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 08/08/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	CERCLE
Débutants Géométrie	CERCLES INSCRITS …				Glossaire Géométrie
INDEX Cercles Triangles	Index	Inscrit	SANGAKUS	Deux cercles – Triangle
	Introduction	Inscrit (suite)	Jumeaux	Deux cercles – Carré
	Puissance	Circonscrit	Carré max	Deux cercles – Carré et triangle
		Exinscrits	Face à face	Trois cercles – Construction
				Trois cercles – Tr. Équilatéraux
				Quatre cercles – Construction
		Sommaire de cette page >>> Problème >>> Démonstration >>> Propriétés de cette figure

Triangle rectangle, carré et deux cercles

Exprimer le côté du carré en fonction des rayons des cercles.

Une démonstration pas si facile à trouver !

Problème
Construction Un triangle rectangle, son carré inscrit sur les côtés de l'angle droit et des deux cercles inscrits dans les deux triangles résultants. Propriété à démontrer

Démonstration

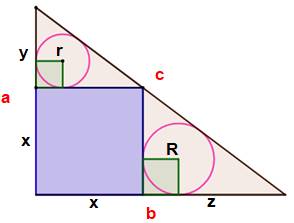
Tactique

Calculer l'aire du petit triangle du haut en fonction de r, et y injecter la valeur de R en profitant des similitudes.

Aire du triangle

Évaluation de deux façons:

Avec les côtés
Avec le rayon du cercle inscrit
Rapprochement
Valeur de x

Similitude

Évaluation de y en introduisant R. On exploite la similitude des deux petits triangles qui implique le même rapport d'homothétie pour les deux cercles.

Similitude
Valeur de y

Retour à la valeur de x et remplaçant y

Équation en x

Racine

Choix

Seule la racine avec "+" est positive. En effet x > R > r

Propriétés de cette figure
Carré inscrit
Cercle inscrit
Similitudes
Aires des deux triangles
Commentaires	Je suis passé par tous ces calculs avant de trouver la solution présentée. J'ai mis un certain temps à me résoudre à considérer les longueurs y et z !

Cas du triangle (3, 4, 5)

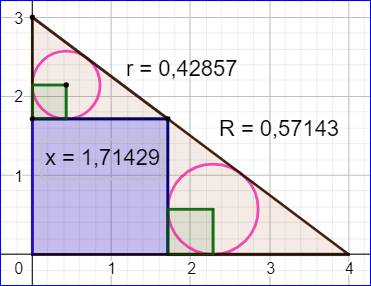
Voir Ce triangle

Suite	Sangakus Rayon du cercle circonscrit Cercle inscrit Puissance d'un point par rapport à un cercle
Voir	Bissectrices Cercle – Index Cercles et triangles Cône	Diamètre Géométrie – Vocabulaire Périmètre Sphère
Sites	Empilement des cercles dans un carré – Wikipédia Deux disques dans un carré – Université de Lyon – Proposition de travaux Empilements dans le plan – Descartes et les Mathématiques Olympiades académiques 2008 – Descartes et les Mathématiques Olympiades académiques de première – 2002 – Académie de Poitiers – Propose plusieurs solutions 11) Sangakus : 2 cercles tangents dans un carré –Mathieu Morinière Sangaku – Cut The Knot – Réflexions et Index d'accès à de nombreux Sangakus
Cette page	http://villemin.gerard.free.fr/GeomLAV/Cercle/DeuxCeTr.htm