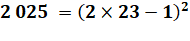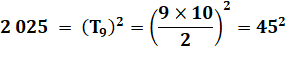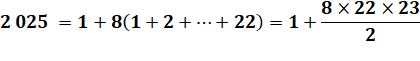|
Création du: 14/10/2024 Édition du: 17/02/2025 |
|
Dictionnaire des Nombres |
|||
|
1 / 10 / 50 / 100 / 500
/ 1000 / 1500 / 1900 / 2000 / 2016 / 2017 / 2018
/ 2019 / |
2025 |
2031 à
2099 / 3000 / 5000 / 10 000 / 20 000 / 50 000 / 100 000 / 106 / 109
/ 10100 Autres |
|
|
2020 / 2021 / 2022
/ 2023 / 2024 / 2025 / 2026 / 2027 / 2028
/ 2029 / 2030 |
|||
Index 2025 – ONZE pages pour ce nombre exceptionnel
|
Nombre 2025 |
||
|
Humour
2024-2025 |
Chiffres de
2025 (jeu) |
Faites
un double-clic pour un retour en haut de
page
Généralités
|
2 025 |
Nombre géométrique de diverses façons:
Voir Nombres géométriques |
|
|
|
|
|
|
1092025 = 1045² => |
01, 09, 2025 concaténés en 102025. |
|
|
Âge carré Les
personnes nées en 1980 ont 45 ans en 2 025, un âge
qui est la racine carrée de l'année en cours. Il faudra
attendre une naissance en 2070 pour que cela se reproduise avec 46 ans. Auguste De Morgan est né en
1806 et il a eu 43 ans en 1849 = 43². Voir Carré de
l'âge |
||
Détails
|
Nombres 2025 et carrés |
||
|
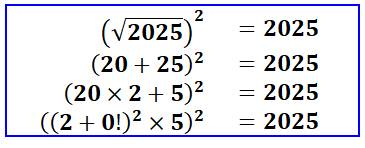
Produit
de deux carrés |
2 025 = 34 × 52 =9² × 5² |
|
|
Nombre
carré Somme
des chiffres: carrée |
2 025 = 45² 2 + 0 + 2 + 5 = 9 = 3² |
|
|
Carrés
voisins |
44² = 1 936 et
46² = 2 116 |
|
|
Plus
petit carré en 20… Seul
en 20xy (à quatre chiffres) |
45²; 20 164 = 142²; 20 449 = 143²; … |
|
|
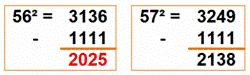
Chaque
chiffre augmenté de 1 => Carré |
2 025 + 1111 = 3136 = 56² |
|
|
Nombre de Kaprekar. |
20 25 = 45² 20 + 25 = 45 |
|
|
Une
fois par jour, on retrouve cette heure. Il y a 34 heures-minute du type carré
dans une journée. |
20:25 |
|
|
Selon
le théorème des deux carrés de Fermat: un entier est la somme de deux carrés si,
et seulement si, chacun de ses facteurs premiers de la forme 4k + 3
intervient avec un exposant pair. Le
théorème de Carl Jacobi
précise que, pour 2025, cette somme de deux carrés est unique |
2 025 = 34 × 52 2 025 = 27² + 36² |
|
|
Le
plus petit carré qui peut s’écrire comme une somme de 17 carrés distincts.
C'est la somme des seize premiers nombres au carré augmenté du carré de 23. |
2 025 = 1² + 2² + … + 16² + 23² = 1
496 + 5 269 |
|
|
Sur
une grille unitaire, un cercle de rayon 26 centré sur un carré de la grille
englobe 2025 carrés. |
|
|
NOMBRES devenant carré
en leur ajoutant un repunit
ou carré moins repunit
|
2 025 + 1111 = 3136 = 56²
|
Le nombre 2025 devient carré en lui ajoutant un repunit de quatre chiffres. Les
nombres ayant cette propriété se calculent facilement comme le montre ces
deux exemples. |
|
|
Un chiffre |
3, 8 |
|
|
Deux chiffres |
14, 25, 38, 53, 70, 89 |
|
|
Trois chiffres |
114, 145, 178, 213, 250, 289, 330, 373, 418, 465, 514, 565, 618, 673, 730, 789, 850, 913, 978 |
|
|
Quatre chiffres |
1005, 1098, 1193, 1290, 1389, 1490, 1593, 1698, 1805, 1914, 2025, 2138, 2253, 2370, 2489, 2610, 2733, 2858, 2985, 3114, 3245, 3378, 3513, 3650, 3789, 3930, 4073, 4218, 4365, 4514, 4665, 4818, 4973, 5130, 5289, 5450, 5613, 5778, 5945, 6114, 6285, 6458, 6633, 6810, 6989, 7170, 7353, 7538, 7725, 7914, 8105, 8298, 8493, 8690, 8889, 9090, 9293, 9498, 9705, 9914 |
|
|
Cinq chiffres |
11389, 11690, 11993, 12298, 12605, 12914, 13225, 13538, 13853, 14170, 14489, 14810, ... |
|
|
Nombres 2025 et cubes |
||
|
N'est
pas une année cube. Les années de type
cube avant et près: |
123
= 1728 133
= 2197 |
|
|
Somme
des cubes des neuf premiers nombres. Aussi le carré le la somme des neuf
premiers nombres, ce qui est aussi le carré du neuvième nombre triangulaires. Ces
trois égalités se retrouvent pour toute somme des k premier nombres (Théorème
de Nicomaque). |
2 025 = 13 + 23 + 33
+ 43 + 53 + 63 +73 + 83
+ 93 2 025 = (1 + 2 + 3 + 4 + 5 + 6 +7 + 8 + 9)² 2 025 = T9² |
|
|
Son
cube est un carré. Le
cube amputé d’un chiffre est un carré. Le
cube divisé par 9 (la somme des chiffres de 2025, qui est un carré. |
2 0253 = 91 125² = 8 303 765 625 28 875² = 8 33 765 625 8 303 765 625 / 9 = 30 375² |
|
|
Nombres 2025 et triangulaire |
||
|
Le
nombre 2025 est somme de deux nombres triangulaires consécutifs. Un
carré est toujours somme de deux nombres triangulaire consécutifs. |
|
|
|
C'est
le carré d'un nombre triangulaire |
|
|
|
Devient
triangulaire
en ajoutant ses deux moitiés. |
20 + 25 = 45 = T9 |
|
|
Le
nombre 2025 est octogonal
centré avec 22 couches plus un élément central. Tous
les octogonaux centrés sont des carrés |
|
||
|
Nombre
octogonal Le nombre 2025 peut être représenté par
un ensemble de points qui forment des octogones
réguliers concentriques de côtés: 1, 2, 3, …23. Formule
de calcul C8,23
= (2n – 1)² = (2 × 23 – 1)² = 13² = 2025
(illustration) Quantité
de points par couche: Après le nombre 1, ce sont tous les multiples de 8 jusqu'à 22. Le dernier étant: 22 x
8 = 176. |
Représentation
|
||
SUITE SUR LE
NOMBRE 2025 voir index en Haut de page (ou double-clic)
|
Retour |
|
|
Suite |
|
|
Sites |
|
|
Cette page |
