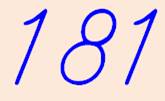Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 01/02/2025 M'écrire Brèves de Maths

DicoNombre Débutant Glossaire Types de nombres Nombres géométriques Nom des nombres Écriture des nombres Table des facteurs Nombres et anglais Langues	Dictionnaire des Nombres
	1 / 10 / 50 / 70 / 80 / 90 / 100 / 110 / 120 / 130 / 140 / 150 / 160 / 170 / 171 / 172 / 173 / 174 / 175 / 176 / 177 / 178 / 179 / 180	181	182 / 183 / 184 / 185 / 186 / 187 / 188 / 189 / 190 / 191 / 192 / 193 / 194 / 195 / 200 / 250 / 300 / 400 / 500 / 600 / 1000 / Autres

Cent-quatre-vingt-un

One hundred (and) eighty-one

Orthographe / Langues

Facteurs
Binaire	1011 0101
Romain	CLXXXI

Suite en propriétés arithmétiques

Congruent

Déficient

Dihédral

Docile (amenable)

Impair

Nombre bon

Palindrome

Premier (42^e)

Premier de Chen

Premier de Pythagore

Premier de Ramanujan

Premier faible

Premier jumeau avec 179

Premier pointé

Premier régulier

Strobogrammatique

Tétradique

Géométrique

18-gonal centré

Carré centré (10^e)

Dodécagonal centré

Hexagonal concentrique (11^e)

Nombre étoilé (6^e)

Pentagonal centré (9^e)

Ce nombre est tétradique premier (lisible dans tous les sens)

Nombre	181 nombres de 0 à 999 contenant au moins un 0. Il y en a 271 ayant au moins un autre chiffre comme le 5.	>>>
Histoire	Résolution 181 de l'ONU - 1947 Partage de la Palestine ratifiée par 33 pays. Création de l'état d'Israël	>>>

Facteurs
Binaire	1011 01012
Ternaire	202013
Bases	13112
Romain	CLXXXI

Nombre premier palindrome, jumeau avec 179

Palindrome en base 10 et 12.

N'est repdigit dans aucune base.

Chiffres et numération

181 18181	Nombre premier ondulant en 1 et 8. Le suivant a 5 chiffres et ensuite 77 chiffres.
181 + (1+8+1) = 191	Avec la somme de ses chiffres, désigne le nombre premier suivant. Tous deux palindromes.
181 – (1+8+1) = 171	Devient palindrome en retirant la somme de ses chiffres.

Addition et soustraction

181 = 29 + 31 + 37 + 41 + 43	Somme de 5 premiers consécutifs.
181 = 2 + 3 + 7 + 78 + 91 & 1/2 + 1/3 + 1/7 + 1/78 + 1/ 91 = 1	Nombre bon.

Avec les puissances

181 = 9² + 10² = 1² + 6² + 12² = 6² + 8²+ 9² = 2² + 2² + 2² + 13²	Nombre binomial. Somme de carrés de nombres consécutifs. Autres sommes de carrés >>>
181 = 2² + 2² + 2² + 13²	Somme de carrés de nombres premiers.

En puissance

181^2 = 105^3 – 104^3 = 1 157 625 – 1 124 864 = 32 761	Une solution de l'équation diophantienne: x^2 = y^3 – z^3
181^2 – 2^15 = 181^2 – 8^5 = 181^2 – 32^3 = 32 761 – 32 768 = – 7	Petit écart entre puissances (rare).
181² = 12 × 13 × 14 × 15 + 1 = 32 761	Produit de quatre nombres consécutifs plus 1 (toujours un carré). Dernier de ce type dans le DicoNombre

Dénombrement, jeux et curiosités

Jeu du quatre 4.

Autour du nombre

Le produit de quatre nombres consécutifs plus 1 est un carré.

1/ 181 = 0,0055248618 7845303867 4033149171 2707182320 4419889502 7624309392 2651933701 6574585635 3591160220 9944751381 2154696132 5966850828 7292817679 5580110497 2375690607 7348066298 3425414364 6408839779 00552486 …

Nombre premier long. La période du développement décimal de la fraction est maximale (180) en une seule suite permutée pour toutes les fractions avec ce dénominateur.

Équation diophantienne de Ramanujan-Nagell

Seulement cinq solutions en (x, n):

1² + 7 = 2³ = 8

3² + 7 = 2⁴ = 16

5² + 7 = 2⁵ = 32

11² + 7 = 2⁷ = 128

181² + 7 = 2¹⁵ = 32 768

When x is a positive integer, the number x² + 7 is a power of 2 only in the following case: x = 1, 3, 5, 11, 181.

Conjecturé par Ramanujan en 1913. Prouvée par Trygve Nagell en 1948.

Voir Équations diophantiennes

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération: base, [chiffres]			Repdigit (Brésilien)
181 2, [1, 0, 1, 1, 0, 1, 0, 1] 3, [2, 0, 2, 0, 1] 4, [2, 3, 1, 1] 5, [1, 2, 1, 1] 6, [5, 0, 1] 7, [3, 4, 6] 8, [2, 6, 5] 9, [2, 2, 1] 10, [1, 8, 1] 11, [1, 5, 5]	12, [1, 3, 1] 13, [1, 0, 12] 14, [12, 13] 15, [12, 1] 16, [11, 5] 17, [10, 11] 18, [10, 1] 19, [9, 10] 20, [9, 1] 21, [8, 13]	22, [8, 5] 23, [7, 20] 24, [7, 13] 25, [7, 6] 26, [6, 25] 27, [6, 19] 28, [6, 13] 29, [6, 7] 30, [6, 1] 60, [3, 1]	Aucun

Voir Bases / Brésiliens

Suite	Nombre 182 Voir haut de page
Voir	Nombres par leur nom Empreinte des nombres DicoNombre Junior Historique de ce site et Références Maitres en nombres
Cette page	http://villemin.gerard.free.fr/NombDico/N100a500/Nb181.htm