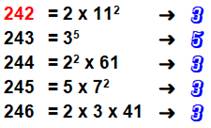Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 02/12/2022 M'écrire Brèves de Maths

Débutant Glossaire Types de nombres Nom des nombres Écriture des nombres Table des facteurs Langues	Dictionnaire des Nombres
	0 / 0,… / 1 / 10 / 50 / 100		200 à 300		300 / 400 / 500 / 600 / 700 / 800 / 900 / 1 000 / 2 000 / 5 000 / 10 000 / 100 000 / 10^6 / 10^9 / 10^100
	200	210	220	230	240	250	260	270	280	290
	240	241	242	243	244	245	246	247	248	249

Faites un double-clic pour un retour en haut de page

Deux-cent-quarante-deux

Two hundred forty two

Nouvelle orthographe

avec des traits d'union partout

Facteurs
Binaire	1111 0010
Bases	222223 14325 4647 20011 BB21
Romain	CCXLII

Suite en propriétés arithmétiques

ABA

Composé

Cunningham

Déficient

Fourchette ou gapful

Non-totient

Pair

Palindrome

Chiffres et numération

242 + 242 = 484 = 22²

Devient palindrome et carré en lui ajoutant son retourné.

Addition et soustraction

242 = 17 + 18 + … + 27 242 = 59 + 60 + 61 + 62	Les deux sommes de nombres consécutifs >>>
242 = 44 + 55 + 66 + 77	4 palindromes consécutifs.

Multiplication et division

242 = 2 x 11^2 243 = 3^2 x 3^3 = 3^5 244 = 2^2 x 61 245 = 5 x 7^2	Première succession de quatre nombres avec facteurs carrés. Liste en fonction de la quantité: [1, 4], [2, 8], [3, 48], [4, 242], [5, 844], [6, 22020]
242 = 11 x 22	Palindrome produit de 2 palindromes consécutifs.
242 / 22 = 11	Nombre fourchette.
242 = 2 x 11^2	Nombre ABA
242 = 2 × 11² 243 = 3² × 27 244 = 2² × 61 245 = 5 × 7²	Quatre nombres successifs divisibles par un carré. Le plus petit.

(242) = t(243) = t(244)

=

Quadruplets de nombres consécutifs ayant même quantité de diviseurs.

Facteurs de 242 = {2, 11}

+ 10 => {12, 21} qui divisent 242 + 10 = 252

Nombre facteur-diviseur.

Plus petit cas pour lequel la fonction de Moebius vaut [0, 0, 0, 0].

Relation croisée entre la somme des diviseurs et le totient.
Idem pour: 9, 225, 242, 516, 729, 3872, …

Avec les puissances

242 = 11² + 11² = 2 x 11² = 1² + 4² + 15² = 3² + 8² + 13² = 7² + 7² + 12²

Toutes les sommes de deux et trois carrés. Il a 27 sommes de quatre et cinq carrés comme: 2 x 5² + 3 x 8² ou 4² + 2(7² + 8²). Autres sommes de carrés >>>

En puissance

242^3 x 2 = 5324² 20402^3 x 2 = 4121204² 2004002^3 x 2 = 4012012004² … 242^5 x 2 = 1288408² 20402^3 x 2 = 84080804008² 2004002^3 x 2 = 840080080040008² …	Curiosité avec son cube: deux fois le cube = carré. Motif sans fin en introduisant des 0. Idem avec la puissance 5. Valable pour toutes les puissances impaires. Explication 2 x 242^3 = 2 (2 x 11²)^3 = 2^4 x 11^6 = (2^2 x 11^3)^2
242^3 = 2 x 2 662² 20402^3 = 2 x 2060602² …	Même type de motif, ans l'autre sens.
2^242 = 7 067 388 259 113 537 318 333 190 002 971 674 063 309 935 587 502 475 832 486 424 805 170 479 104 = 7,06… 10^72	La plus petite puissance de 2 avec trois 0 répétés, et avec trois 3 en prime.
2^50 = 1 125 899 906 842 624	Plus petite puissance de 2 avec une suite de trois 0 consécutifs.

Combinatoire et jeux

242 Q = n² – n + 2 avec n = 16 Q(n) = {2, 4, 8, 14, 22, 32, 44, 58, 74, 92, 112, 134, 158, 184, 212, 242, 274, 308, 344, 382, 422, 464, 508, 554, 602,…}	Quantité maximale de régions déterminées par seize cercles dans le plan. Formule et valeurs jusqu'à 25 cercles.
		Jeu du quatre 4. Avec la notation .4 = 0,4 = 2/5

Culture

Transport

242 = 2 (2 + 4 + -2) = 16 roues Exemple de codage des types de locomotives à vapeur: 2 pour un bogie porteur à l'avant (deux essieux), 4 pour quatre essieux moteurs, et 2 pour 2 essieux porteurs à l'arrière.

>>>

Identité détaillée

Voir Diviseurs, Quantité, Somme, Fonctions arithmétiques

Numération: base, [chiffres]			Repdigit (Brésilien)
2, [1, 1, 1, 1, 0, 0, 1, 0] 3, [2, 2, 2, 2, 2] 4, [3, 3, 0, 2] 5, [1, 4, 3, 2] 6, [1, 0, 4, 2] 7, [4, 6, 4] 8, [3, 6, 2] 9, [2, 8, 8] 10, [2, 4, 2] 11, [2, 0, 0]	12, [1, 8, 2] 13, [1, 5, 8] 14, [1, 3, 4] 15, [1, 1, 2] 16, [15, 2] 17, [14, 4] 18, [13, 8] 19, [12, 14] 20, [12, 2] 21, [11, 11]	22, [11, 0] 23, [10, 12] 24, [10, 2] 25, [9, 17] 26, [9, 8] 27, [8, 26] 28, [8, 18] 29, [8, 10] 30, [8, 2] 60, [4, 2]	3, [2, 2, 2, 2, 2] 21, [11, 11] 120, [2, 2] 241, [1, 1]

Voir Bases / Brésiliens

Retour Suite	Nombre 241 Nombre 243
Voir	Nom des nombres Nombres géométriques
Voir	Nombres par leur nom Empreinte des nombres DicoNombre Junior Historique de ce site et Références Maitres en nombres

Cette page

http://villemin.gerard.free.fr/NombDico/N100a500/Nomb200/Nb242.htm