|
|||||||||||||||||||||||||||||||
![]()
|
Méthode de PHERU
C'est la première publication indienne
connue à ce jour.
|
Voir
approche en Observation
sur carré d'ordre 3 / Truc de B. Franklin
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
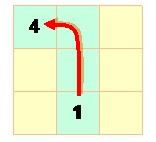
Étape
1
Étape
2
|
Colonne centrale
Mouvement du cavalier
Remplissage complet avec illustration de l'effet d'enroulement |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Étape
1
Étape
2
Propriétés
de ce carré magique
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
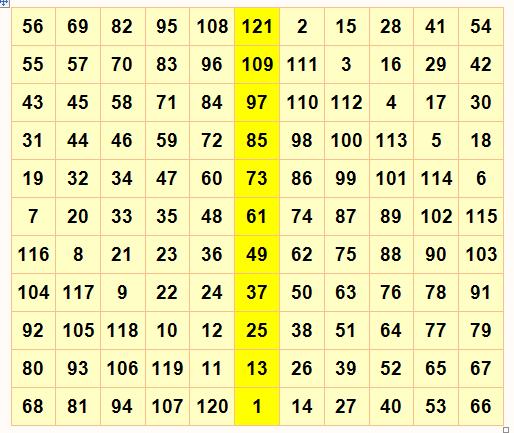
Somme magique: 175 Associatif, mais pas panmagique. |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Somme magique: 369 Associatif, mais pas panmagique. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Suite |
|
|
Voir |
|
|
Diconombre |
|
|
Sites |
|
|
Cette page |
![]()