|
|||||||||||||||||||||||||||||||||||
![]()
|
ENTIERS IMPAIRS & CUBES Tout cube est
Exemple
de propriété 43 = 64
= 13 + 15 + 17 10²
– 6² |
|
|
|
|
Approche
avec un exemple
|
|
|
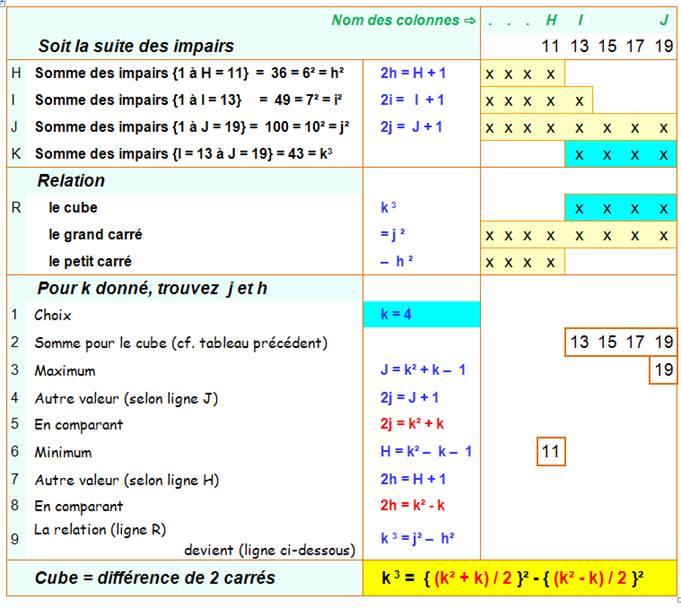
Théorème Le cube d'un nombre k est la somme des nombres impairs de k² - k + 1 à k² + k – 1 Les
plages (I, J) pour les cubes de 1 à 20 k I
= k² - k + 1 J = k² + k - 1 1 1 1 2 3 5 3 7 11 4 13 19 5 21 29 6 31 41 7 43 55 8 57 71 9 73 89 10 91 109 11 111 131 12 133 155 13 157 181 14 183 209 15 211 239 16 241 271 17 273 305 18 307 341 19 343 379 20 381 419 Lecture: 203 = 381 + 383 + 385 + … 417 + 419 |
Voir Table
|
|
|
|
43
= 4x4 + 4x4 + 4x4 + 4x4
43 = 1x4x4 + 1x4x4 + 1x4x4 + 1x4x4
43 = 1x4x(4-3) + 1x4x(4-1) + 1x4x(4+1) + 1x4x(4+3) 43 = 1x4x1 + 1x4x3 + 1x4x5 + 1x4x7
43 = 4 (1 + 3 + 5 + 7)
= 4 + 12 + 20 + 28
53 = 5 (1 + 3 + 5 + 7 + 9)
= 5 + 15 + 25 + 35 + 45 |
|
|
|
|
|
Approche
avec un exemple
|
|
|
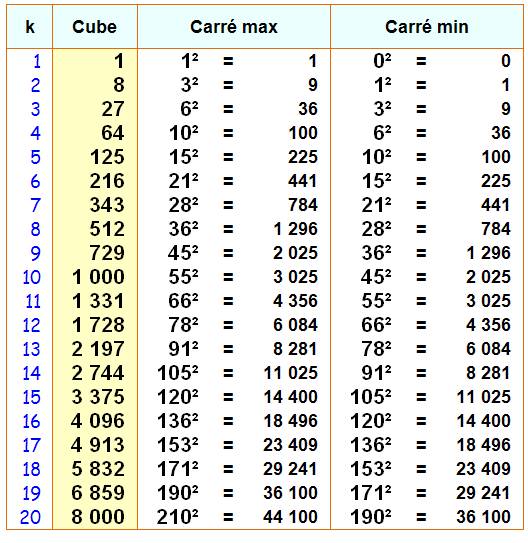
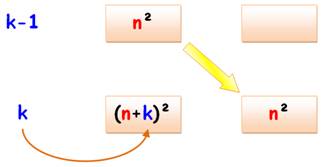
Théorème Le cube d'un nombre k est la différence des carrés de ½ (k²+ k) et ½ (k²– k). Valeurs
pour les cubes de 1 à 20
203
= 210² – 190² = (190 + 20)² – 190² Littéralement:
retrouver les nombres au carré à partir du cube de k k3 = (n + k )² – n² = n² + 2nk + k² - n² = k (2n + k) k2
= 2n + k n = ½ (k² - k) Pour k = 20, on retrouve n =
½ (400 – 20) = 190 |
Voir Cube = Différence de carrés de nombres successifs
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()