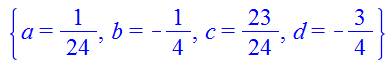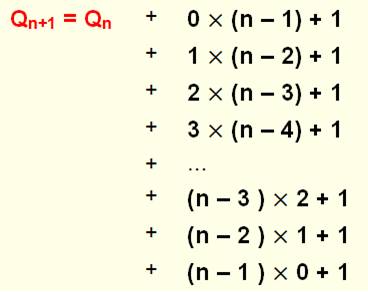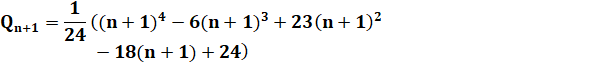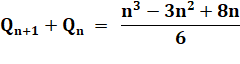|
||||||||||||||||||||||||||
![]()
|
DIVISION
DU CERCLE EN RÉGIONS Où l’on montre que l’extrapolation
n’est pas toujours justifiée. A
l’usage des professeurs et, comme idée de travaux
pratiques. Démarche Nous
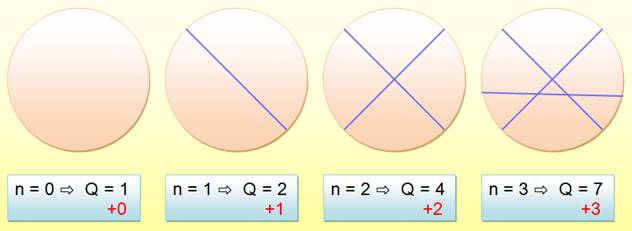
allons d'abord compter, puis établir la relation Qn = f(n), Q étant la quantité de régions et n le nombre de points sur le cercle. Nous
allons ensuite justifier ces quantités en établissant la formule itérative: Qn+1 = Qn + g(n); Pour
cela nous aurons besoin de travailler sur le cas de la partition du cercle
par des cordes. En effet, chaque nouveau point sur le cercle engendre une certaine
quantité de cordes et chaque corde partage
les régions existantes. |
Voir Toutes les autres possibilités de partager
le cercle
|
|
|
|
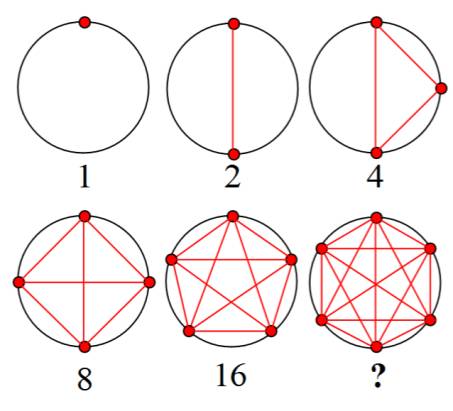
Problème du cercle de Moser Soit n
points sur un cercle. On trace toutes
les droites possibles rejoignant ces points. Quel est le
nombre de parts découpées dans le cercle ?
Il
faut trouver le nombre suivant Fausse piste
On remarque que
la succession des nombres donne les puissances de
2. Le suivant serait
32? Faux ! Voir Grande loi de Guy
Les points sur le
cercle doivent être distincts. Les droites tracées doivent couper les autres,
sans passer un point d'intersection existant. |
|
|
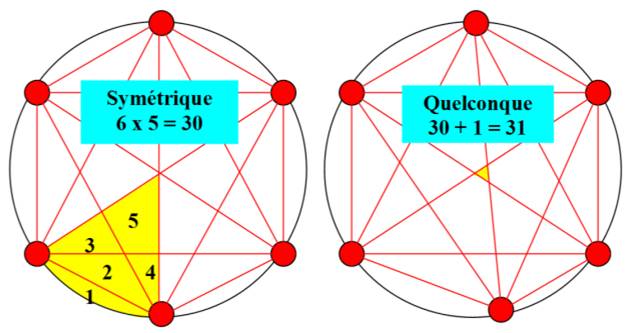
Réponse C’est 31 dans le
cas général. et 30 si
l’hexagone formé est régulier.
|
|
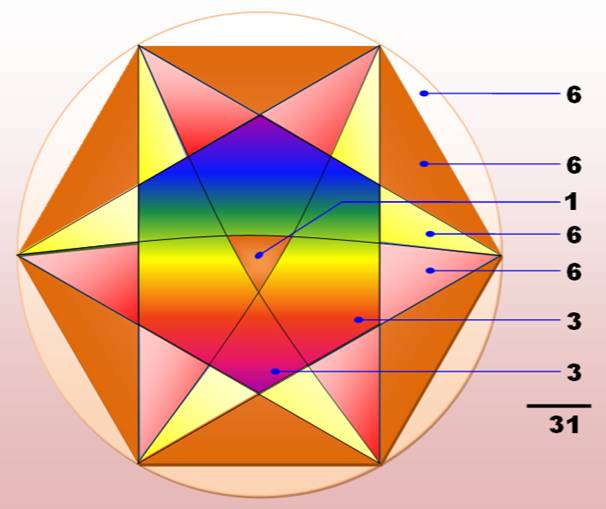
Vue symétrique artistique |
|
|
|
|
|
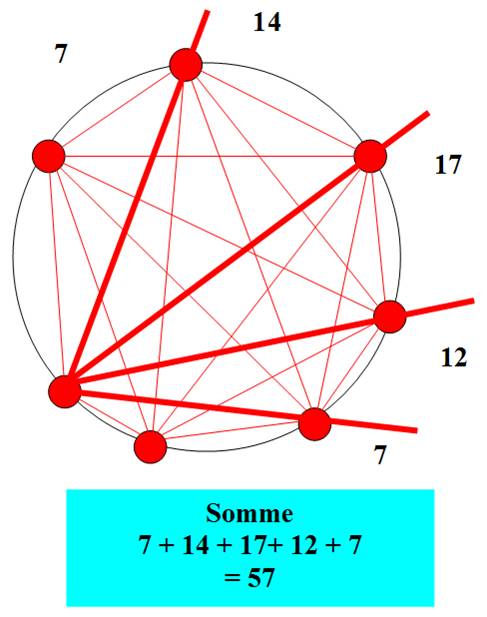
Cas de 7 points
|
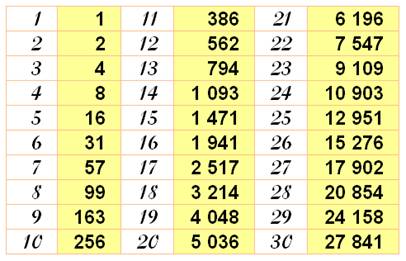
Formule et valeurs
|
N
est la quantité de portions obtenues en partageant un cercle avec n sécantes
quelconques.
Note:
on retrouve une puissance de 2 avec 10 sécantes. |
Voir Divisibilité par 24
|
|
|
|
Q = a.n4
+ b.n3 + c.n2 + d.n + e Q0 = 1
Q1 =
1.a + 1.b + 1.c + 1.d + 1 = 1 Q2 =
16.a + 8.b + 4.c + 2.d + 1 = 2 Q3 =
81.a + 27.b + 9.c + 3.d + 1 =
4 Q4 = 256.a + 64.b + 16.c + 4.d + 1 = 8
Linear({a+b+c+d,16*a+8*b+4*c+2*d-1,81*a+27*b+9*c+3*d- 3,256*a+64*b+16*c+4*d-7},{a,b,c,d});
Notons que nous obtenons la formule sans justifier les valeurs. Pour y
arriver il nous faut compter les partitions avec des cordes.
Objet du paragraphe suivant. |
|
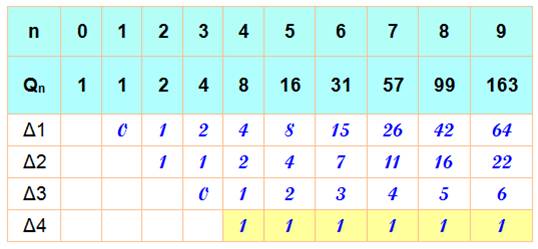
Voir Calcul de la formule par la méthode
des différences et coefficients binomiaux
Merci à
Jean-Jacques Juré pour m'avoir signalé cette possibilité "élégante"
dont les calculs sont simples
|
|
|
|
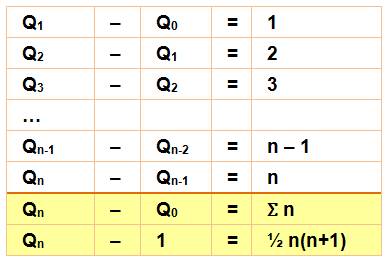
Qn+1 = Qn + (n + 1) Qn+1 – Qn = n + 1
Qn = ½ n (n + 1) + 1 |
|
Anglais: What is the maximum number of regions you can have
with n chords in a circle?
|
|
|
|
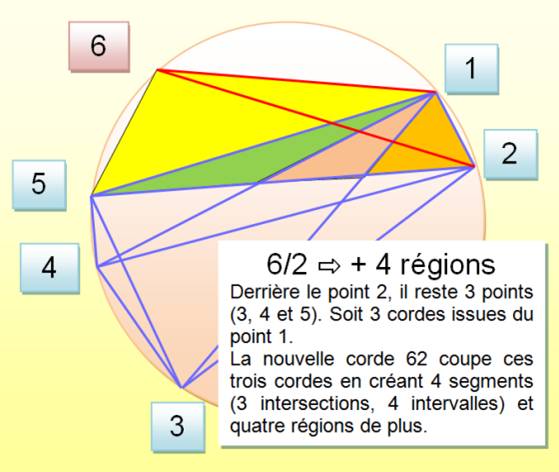
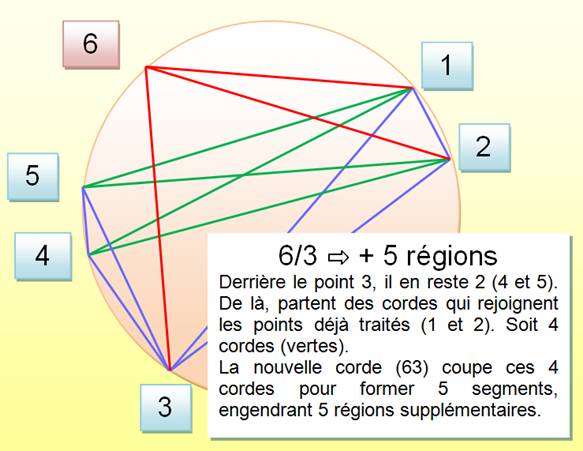
Principe du dénombrement avec
6 points
|
|
|
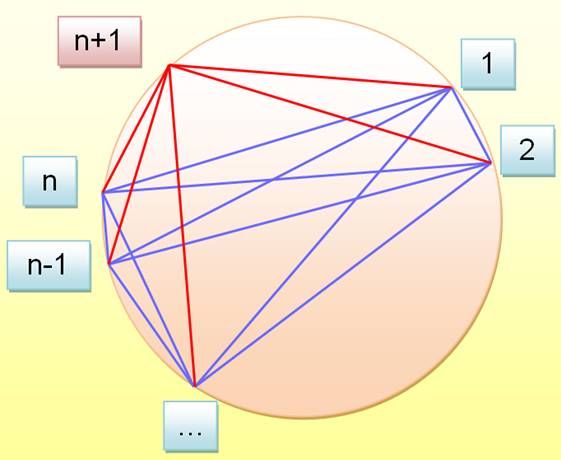
Principe du dénombrement – Cas général de n points
|
|
Finalisation
|
![]()
|
Retour |
|
|
Voir |
|
|
|
|
|
Cette page |
![]()