|
|||||||||||||||||||||||||||||
![]()
|
Dimensions – 4D et plus Nous évoluons dans un monde
à trois dimensions. Dire que le temps doit être considéré comme une quatrième dimension, passe
encore, mais dire que l'espace compte en fait quatre dimensions, c'est plus dur à
imaginer. Nous allons donner quelques
pistes aidant à comprendre l'existence d'une quatrième dimension. |
Anglais:
fourth-dimensional geometry
|
|
||
|
|
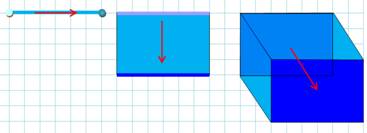
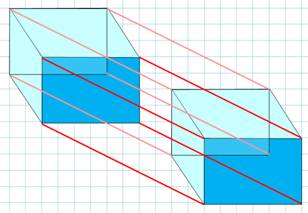
Passer d'une dimension à la suivante consiste à faire
glisser un objet de dimension inférieure et d'en garder la trace.
Passer à la quatrième dimension consiste à garder la
trace du déplacement d'un objet à trois dimensions. |
|
|
|
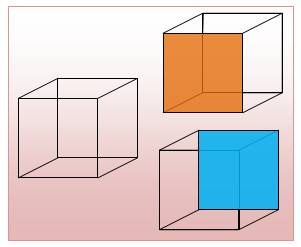
Image ambigüe du cube
Frise avec cubes de Necker
Merci à Pauline (10 ans)
pour son dessin |
|
|
||
|
|
|
|
|
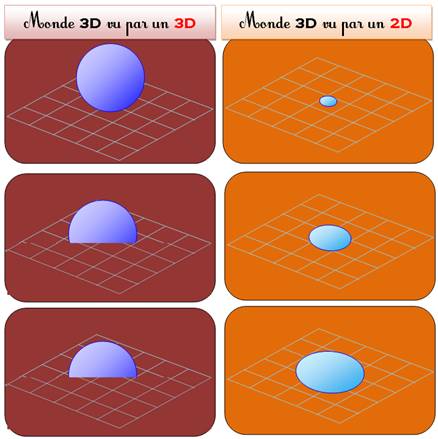
Cette
analogie figure dans le célèbre livre Flatland de E. Abott à la page 98 |
Charles Hinton, imagine lui,
une spirale qui traverse le
pays plat. Les habitants observent un point qui se déplace le long de la
circonférence d'un cercle imaginaire. |
|
|
|
||
|
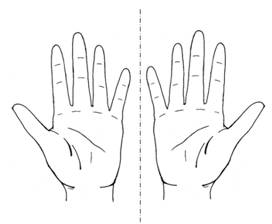
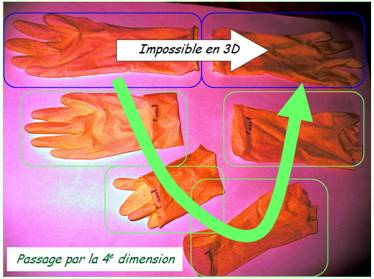
Pour obtenir de ma main gauche qu'elle devienne exactement ma main
droite, il faudrait imaginer qu'elle est comme un gant en caoutchouc que l'on
retournerait. Pour cela, il faudrait que ma main gauche se désintègre et que chaque atome reprenne une place symétrique lors de la
reconstitution. Alors cette nouvelle main serait une main droite. |
En négligeant l'épaisseur des mains, une simple rotation autour de
l'axe permet de passer d'une main à l'autre. Essayez: paumes vert le haut, vous refermez simplement les mains pour
les retrouver en mains-jointes. Oui, mais, elles restent symétriques (paume
contre paume) et non pas identiques! Vous n'êtes pas le génie.
|
|
|
|
|||
|
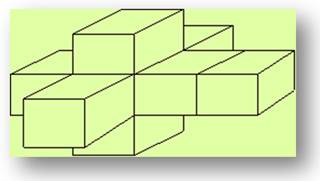
En géométrie, on
connait l'hypercube
(tesseract) ou l'hypersphère. La
quatrième dimension s'applique évidemment à toutes les formes géométriques.
Les mathématiciens savent également se projeter dans la cinquième dimension,
la sixième, … Dans ces mondes, les
surfaces sont des variétés géométriques (anglais: manifold).
Et les volumes sont des polytopes. |
Hypercube développé (patron)
|
||
|
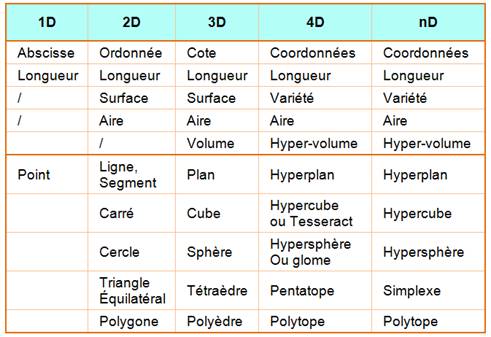
Dimensions et leur vocabulaire Note: le mot glome pour une hypersphère en 4D est plutôt
anglais. Voir
|
|
||
Les géométries
|
Selon le postulat
de départ, il existe trois
géométries différentes. Chacune peut s'appliquer
aux trois dimensions habituelles ou être étendues à des dimensions
supérieures. |
|
En algèbre, les quaternions
caractérisent un monde à quatre dimensions comme les nombres complexes le font pour
deux. |
|
|
En théorie des nombres,
le groupe
monstre s'élève dans un monde à 196 884 dimensions! Représentation (à droite) du
groupe E8, un cousin
du groupe monstre. |
|
|
En physique, la théorie de la relativité introduit une
quatrième dimension: le temps qui doit être vu à un coefficient près (la vitesse de la lumière), comme une
distance. Dans l'espace-temps, il
existe un invariant reliant les quatre dimensions: x² + y² + z² - ct² = H² Une sorte de généralisation
du théorème de Pythagore. |
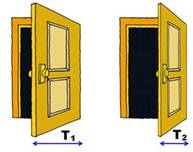
La taille de la porte dépend de la l'ouverture de la porte, pourtant
c'est toujours la même porte. Voir Analogie de la porte entr'ouverte |
|
La mécanique quantique
cherche à modéliser le monde microscopique des atomes, des électrons, des quarks, des cordes … Les physiciens n'hésitent
pas à se plonger dans des mondes à onze dimensions comme c'est le cas pour la
théorie des super-cordes. |
|
Quatre dimensions
|
D'une manière
générale, quatre dimensions impliquent quatre grandeurs, quatre degrés de liberté, pour définir quelque
chose. Par exemple,
|
|
|
||
|
(-428 à -348) |
Avec son mythe de la
caverne, Platon projette un monde
tridimensionnel sur un mur bidimensionnel. |
|
|
(-384 à -322) |
Aristote imagine la ligne, le
plan et le solide et rien d'autre au-delà. Idée qu'on doit se
faire des grandeurs; la ligne, la surface et le solide; idée qu'on doit se
faire de l'univers et de l'ensemble des chose (Du Ciel). |
|
|
(-150) |
Ptolémée tente de prouver que la
quatrième dimension n'existe pas |
|
|
(Vers 8 à 64) |
Saint Paul cite
quatre grandeurs. En sorte que (…)
vous puissiez comprendre avec tous les saints quelle est la largeur, la longueur, la profondeur et la hauteur,
et connaître l'amour de Christ, qui surpasse toute connaissance, … Lettre de saint Paul aux Éphésiens 3:17à19. |
|
|
(1320-1382) |
Oresme invente le système de coordonnées.
Il y en a trois, mais pas quatre. |
|
|
(1501-1576) |
Cardan pense qu'il n'y a pas d'objet
représenté par la puissance quatre. La positio (la
première puissance) correspond à une ligne, le quadratum (le carré) à une
surface, and le cubum (le cube) à un corps solide, la nature ne permet pas
d’aller au-delà. |
|
|
(1540-1603) |
Viète n'hésite pas à traiter les équations d'ordre supérieur à 3, alors
qu'il n'y a pas de contre partie géométrique. |
|
|
(1538-1612) |
Clavius tente de démontrer
qu'il n'existe pas plus de trois perpendiculaires entre elles
dans l'espace, comme les trois arêtes d'un
cube issues d'un même sommet. |
|
|
1614-1687 |
Le premier philosophe à
imaginer le concept de quatrième dimension. Dans son livre L'immortalité de l'âme, il introduit
cette dimension (the spissitude) pour y loger l'âme, l'esprit. |
|
|
(1616-1703) |
Wallis constate que l'algèbre est
indépendante de la géométrie. On ne peut
multiplier un cube par son côté.
Il en conclut que l’algèbre, autorisant des puissances quelconques, repose
sur l’arithmétique et non sur la géométrie. Il qualifie les
dimensions supérieures de monstres de la nature, moins vraisemblables que les
chimères ou les centaures. |
|
|
(1724-1804) |
Kant postule que l’espace
avec ses caractéristiques est une propriété de notre conscience et non du monde extérieur. Ni l'espace, ni le temps, ne peuvent être réellement perçus.
Ce sont des éléments que les humains utilisent pour structurer leurs
expériences. |
|
|
(1717-1783) |
D'Alembert prétend que le temps
est une quatrième dimension. On dit qu'il n'est
pas possible de concevoir plus de trois dimensions. Un homme d’esprit de ma
connaissance croit qu’on pourrait cependant regarder la durée comme une
quatrième dimension. Mais c'est aussi une sensation. |
|
|
(1736-1813) |
Lagrange aussi pense que le temps est
une quatrième dimension. Dans son livre:
Théories des fonctions analytiques (1797). |
|
|
(1790-1868) |
Moebius découvre que l'image dans
un miroir est obtenue par une rotation de l'original dans un espace à quatre
dimensions. Première
utilisation mathématique de cette dimension. |
|
|
(1801-1887) |
Livre: L'espace a quatre dimensions (1846), une partie de Quatre paradoxes Utilisation de créature 2D,
non conscience de la 3D, et de la projection de leur ombre. Le temps est leur
troisième dimension |
|
|
(1814-1897) |
Sylvester utilise les matrices
pour étudier les géométries à plusieurs dimensions. Il introduit le
terme matrice en
1850 (du latin mater). |
|
|
(1821-1895) |
Livre de Cayley: Géométrie analytique à n dimensions |
|
|
(1826-1866) |
La
géométrie de Riemann est un
espace 3D sphérique. Par ailleurs, il a conçu une théorie des géométries non euclidiennes à
n dimensions (Célèbre conférence du 10 juin 1854: une nouvelle
géométrie est née). Cette
mystérieuse géométrie va susciter l'intérêt des philosophes, des écrivains et
des artistes des décennies suivantes. Soixante ans plus tard, c'est Einstein qui va en faire usage pour
modéliser sa théorie de la relativité.
Après une
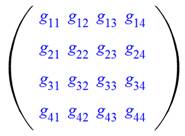
analogie avec un monde 2D, Riemann Il introduit 16
nombres (tenseur métrique) dont 10 sont
indépendants pour caractériser une surface en 4D. Cet outil puissant lui
permit de généraliser aux dimensions supérieures. |
|
|
(1853-1907) |
Le grand philosophe de
l'hyperespace, le pionnier, connu pour ses écrits sur la quatrième dimension. Il explique la
construction de l'hypercube avec 27 cubes colorés. (Gendre du
mathématicien George Boole). |
|
|
(1877) |
Un célèbre procès (1877) qui
popularisa la quatrième dimension. D'éminents
scientifiques (Rayleigh, Thompson, Weber, Crookes...) défendaient l'accusé en
prétendant que ses forfaits faisaient appel à des esprits logés dans la
quatrième dimension. |
|
|
(1884) |
Flatland (le pays plat),
célèbre livre qui raconte le voyage d'un carré dans les dimensions
supérieures. Aussi une satire
de la société victorienne et de la condition de la femme. |
|
|
Poincaré Henri (1854-1912) |
Poincaré (1905) jette les bases
mathématiques de la relativité en introduisant un espace vectoriel à quatre
dimensions. Il
reformule la transformation de Lorentz. C'est à partir des idées de Cayley,
Hertz, Lorentz, Poincaré, Einstein et Planck
que le mathématicien Hermann Minkowski élaborera la théorie de
l’espace-temps, élément essentiel de la découverte par Einstein de la théorie
de la relativité générale. Dans les articles que j’ai précédemment consacrés à l’espace, j’ai
surtout insisté sur les problèmes soulevés par la géométrie non-euclidienne,
en laissant presque complètement de côté d’autres questions plus difficiles à
aborder, telles que celles qui se rapportent au nombre des dimensions. Toutes
les géométries que j’envisageais avaient ainsi un fond commun, ce continuum à
trois dimensions qui était le même pour toutes et qui ne se différenciait que
par les figures qu’on y traçait ou quand on prétendait le mesurer. Henri Poincaré, Valeur de la Science |
|
|
Artistes |
1895 –
H.G. Wells – La machine à explorer le temps. 1900 –
Maurice Princet, le mathématicien du cubisme, introduit le concept de quatrième
dimension dans l'art, profitant des travaux de Poincaré. Il fait partie de
l'école de Paris (Bateau-Lavoir à Montmartre) avec d'autres comme Pablo
Picasso, Guillaume Apollinaire, Max Jacob, Jean Metzinger, Marcel Duchamp … 1912 –
Albert Gleizes et Jean Metzinger – Livre: Du cubisme avec référence aux
travaux de Riemann. 1912 –
Marcel Duchamp – Tableau: Nu descendant un escalier. 1953 – Salvador Dali – Tableau: Corpus
hypercubus (Crucifixion). Ci-contre Vous trouverez
ce sujet développé en Quatrième
dimension (art) |
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
|
|
|
Sites |
|
|
Vidéo |
Comment
visualiser un espace en 4D au travers de 4 espaces en 3D, illustré par
l'outil en ligne Tak4D
|
|
Cette page |
![]()