NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 21/12/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	CERCLE
Débutants Géométrie	CERCLES INSCRITS …				Glossaire Géométrie
INDEX Cercles Triangles	Index	Inscrit	SANGAKUS	Deux cercles – Triangle
	Introduction	Inscrit (suite)	Jumeaux	Deux cercles – Carré
	Puissance	Circonscrit	Carré max	Deux cercles – Carré et triangle
		Exinscrits	Face à face	Trois cercles – Construction
	Chapelet de cercles			Trois cercles – Carré
				Trois cercles – Tangents
				Trois cercles – Tr. Équilatéraux
				Quatre cercles – Construction
		Sommaire de cette page >>> Les trois cercles

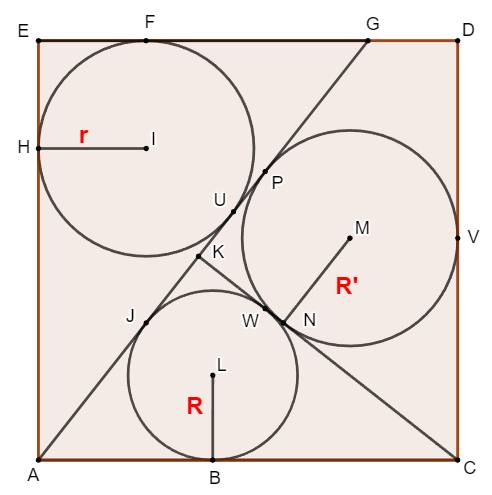
Trois cercles tangents

dans un carré

Problème assez difficile.

Les trois cercles			haut
Construction Un carré, une sécante AG, une perpendiculaire CK. Les cercles tangents dans les espaces créés. Le cercle de centre L a un rayon de 12 cm. Quel est le rayon r ? Remarque L'énoncé de ce problème donne également le rayon R'. Lequel est inutile, d'autant que la valeur donnée par l'énoncé est inexacte (16 cm). Pistes 1) Triangles rectangles ACK et AGE et application du théorème de Pythagore; 2) Ces deux triangles sont semblables et application de la loi des proportions; et 3) Les segments de tangentes comme AB et AJ ou CB et CW sont égaux.
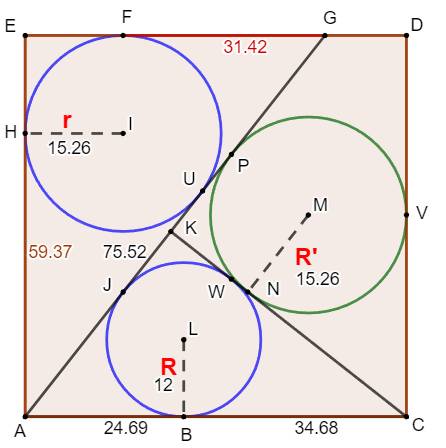
Équations		Résolution avec logiciel de calcul R = 12 (hypothèse) r = 15,26423579 AB = 24,69805232 BC = 34,68064364 FG = 31,41640786
Illustration cotée Notez que le cercle vert est construit facilement: son centre est à l'intersection des bissectrices des angles KCD et GKC. La mesure du rayon donne 15,26143 cm et non la valeur 16 proposée par l'énoncé.

Suite	Sangakus – Autres constructions géométriques Arbelos Carré et deux cercles tangents Cercle inscrit Chaine de Pappus Puissance d'un point par rapport à un cercle Quatre cercles Rayon du cercle circonscrit Sangakus
Voir	Bissectrices Cercle – Index Cercles et triangles Cône Diamètre Géométrie – Vocabulaire Périmètre Sphère
Site
Cette page	http://villemin.gerard.free.fr/GeomLAV/Cercle/TroiCeCa.htm