NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 21/12/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	CERCLE
Débutants Géométrie	CERCLES INSCRITS …				Glossaire Géométrie
INDEX Défis Cercles Triangles	Index	Inscrit	SANGAKUS	Deux cercles – Triangle
	Introduction	Inscrit (suite)	Jumeaux	Deux cercles – Carré
	Puissance	Circonscrit	Carré max	Deux cercles – Carré et triangle
		Exinscrits	Face à face	Trois cercles – Construction
	Chapelet de cercles			Trois cercles – Carré
				Trois cercles – Tangents
				Trois cercles – Tr. Équilatéraux
				Quatre cercles – Construction
		Sommaire de cette page >>> Trois cercles tangents

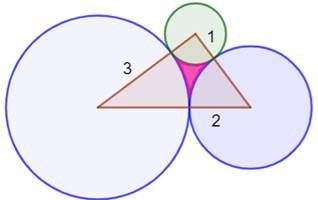
Trois cercles tangents

Aire de la zone centrale ?

Trois cercles sont tangents deux à deux. Ils délimitent une zone centrale en forme de triangle courbe. Quelle est l'aire de cette zone ?

Trois cercles tangents		haut
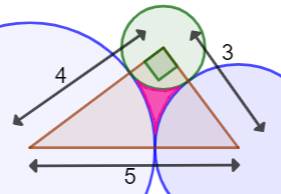
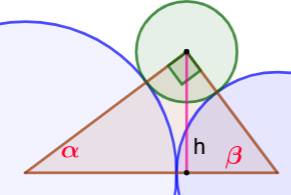
Problème Trois cercles tangents deux à deux de rayon 1, 2 et 3. Ces cercles délimitent une zone centrale rouge dont il faut calculer l'aire. Pistes On a tracé le triangle dont les sommets sont les trois centres des cercles. On remarque immédiatement que les côté du triangle mesurent 3, 4 et 5, ce qui constitue un triangle rectangle remarquable. L'angle droit se trouve au centre du cercle vert. La hauteur h est facilement calculable en fonction des trois côtés: h = produit des côtés de l'angle droit divisé par l'hypoténuse. Alors les angles alpha et bêta sont connus par leur sinus. L'aire cherchée est égale à l'aire du triangle diminuée de l'aire des trois secteurs.
Calculs Remarque Le calcul est relativement simple car nous avons à faire à des mesures (3, 4, 5) qui conduisent à appliquer la réciproque du théorème de Pythagore et, à en déduire que l'angle en vert est droit et, cela permet le calcul de la hauteur. Le calcul serait bien plus complexe sans cette propriété.

Suite	Sangakus – Autres constructions géométriques Arbelos Carré et deux cercles tangents Cercle inscrit Chaine de Pappus Puissance d'un point par rapport à un cercle Quatre cercles Rayon du cercle circonscrit Sangakus
Voir	Bissectrices Cercle – Index Cercles et triangles Cône Diamètre Géométrie – Vocabulaire Périmètre Sphère
Cette page	http://villemin.gerard.free.fr/GeomLAV/Cercle/TroisTan.htm