|
DÉFINITION
|

|
|
N°
|
Catégorie
|
Théorèmes (conjectures et autres propriétés)
|
Niveau
|
Lien
|
|
cl1
|
Classe
|
 Tout nombre pair est de la forme 2k.
Tout nombre pair est de la forme 2k.
 Tout nombre impair est de la
forme 3k.
Tout nombre impair est de la
forme 3k.
|
*
|
>>>
|
|
di1
|
Divisibilité
|
 Un nombre terminé par {0, 2,
4, 6, 8} est divisible par 2. (Nombres pairs).
Un nombre terminé par {0, 2,
4, 6, 8} est divisible par 2. (Nombres pairs).
 Un nombre dont la somme des
chiffres est un multiple de 3 est divisible par 3.
Un nombre dont la somme des
chiffres est un multiple de 3 est divisible par 3.
 Un nombre dont les deux
derniers chiffres forment un nombre divisible par quatre est divisible par 4.
Un nombre dont les deux
derniers chiffres forment un nombre divisible par quatre est divisible par 4.
 Un nombre terminé par {0, 5}
est divisible par 5.
Un nombre terminé par {0, 5}
est divisible par 5.
 Un nombre terminé par 0 est
divisible par 10.
Un nombre terminé par 0 est
divisible par 10.
|
*
|
>>>
|
|
di2
|
Divisibilité
|
 Si m divise ab et si m et a sont étrangers, alors m
divise b.
Si m divise ab et si m et a sont étrangers, alors m
divise b.
Lemme de Gauss
|
**S
|
>>>
|
|
di3
|
Divisibilité
|
 Si a et p sont étrangers, alors
Si a et p sont étrangers, alors 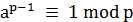
Petit
théorème de Fermat
|
**S
|
>>>
|
|
di4
|
Divisibilité
|
 Le nombre 2p – 2 est
toujours divisible par 2 quand p est premier.
Le nombre 2p – 2 est
toujours divisible par 2 quand p est premier.
Théorème
chinois base du petit théorème de Fermat
|
**
|
|
|
di5
|
Divisibilité
|
 Soit m > 0; si PGCD (a,m) = 1, alors
Soit m > 0; si PGCD (a,m) = 1, alors 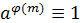 mod m mod m
Théorème
d'Euler (généralisation du petit théorème de Fermat)
|
***
|
>>>
|
|
di6
|
Division
|
 Si a et b sont positifs, b non nul, il existe des entiers
q et r uniques satisfaisant à la fois: a = qb + r
et 0
Si a et b sont positifs, b non nul, il existe des entiers
q et r uniques satisfaisant à la fois: a = qb + r
et 0 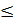 r < b r < b
Définition
de la division
|
*
|
>>>
|
|
di7
|
Divisibilité
|
 Le nombre (n – 1)! + 1 est divisible par n ssi n est premier
Le nombre (n – 1)! + 1 est divisible par n ssi n est premier
Théorème
de Wilson
|
***
|
>>>
|
|
eq1
|
Équation
|
 L'équation diophantienne ax +
by = c admet au moins une solution si d = PGCD (a,b) divise c.
L'équation diophantienne ax +
by = c admet au moins une solution si d = PGCD (a,b) divise c.
|
**
|
>>>
|
|
et1
|
Étrangers
|
 Deux entiers naturels a et b; il existe deux entiers
relatifs u et v tels que au + bv = PGCD (a,b).
Deux entiers naturels a et b; il existe deux entiers
relatifs u et v tels que au + bv = PGCD (a,b).
 Les nombres a et b sont premiers entre eux ssi il existe deux nombres u et v dans
Les nombres a et b sont premiers entre eux ssi il existe deux nombres u et v dans 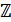 (entiers relatifs) tels que: au + bv = 1. (entiers relatifs) tels que: au + bv = 1.
 Plus généralement, n entiers a1, a2,
... , an non nuls sont premiers entre eux
dans leur ensemble ssi il existe (u1, u2,
... , un) de
Plus généralement, n entiers a1, a2,
... , an non nuls sont premiers entre eux
dans leur ensemble ssi il existe (u1, u2,
... , un) de 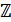 tel que a1u1 + a2u2
+ ... + anun = 1. tel que a1u1 + a2u2
+ ... + anun = 1.
Relations de Bézout
|
***S
|
>>>
>>>
|
|
fa1
|
Facteur
|
 Si PGCD (a,b)
= 1, alors a et b sont premiers entre eux (on dit aussi étrangers, ou
relativement premiers).
Si PGCD (a,b)
= 1, alors a et b sont premiers entre eux (on dit aussi étrangers, ou
relativement premiers).
 Si PGCD (a,b)
= d, alors a/d et b/d sont étrangers.
Si PGCD (a,b)
= d, alors a/d et b/d sont étrangers.
|
**
|
>>>
|
|
fa2
|
Facteur
|
 Le PGCD (a,b)
est le dernier reste non nul trouvé dans la suite itérative des relations: a
= qb + r avec l'itération a := b et b := r.
Le PGCD (a,b)
est le dernier reste non nul trouvé dans la suite itérative des relations: a
= qb + r avec l'itération a := b et b := r.
Algorithme
d'Euclide
|
**
|
>>>
|
|
ge1
|
Géométrie
|
 Un polygone régulier à n côtés est constructible
à la règle et au compas si n est de la forme 2rp1p2...pk
où les pi sont des
nombres premier de Fermat distincts.
Un polygone régulier à n côtés est constructible
à la règle et au compas si n est de la forme 2rp1p2...pk
où les pi sont des
nombres premier de Fermat distincts.
S'applique évidemment à la division du cercle en parts égales.
Trouvé par Gauss
|
***S
|
>>>
|
|
mo1
|
Modulo
|
 Tout nombre divisé par 2
donne { 0, 1} comme reste.
Tout nombre divisé par 2
donne { 0, 1} comme reste.
 Tout nombre divisé par 3 donne
{-1, 0, 1} comme reste.
Tout nombre divisé par 3 donne
{-1, 0, 1} comme reste.
 Tout nombre divisé par 5
donne {-2, -1, 0, 1, 2} comme reste.
Tout nombre divisé par 5
donne {-2, -1, 0, 1, 2} comme reste.
 Etc.
Etc.
|
*
|
>>>
|
|
mo2
|
Modulo
|
 Si une opération est juste,
son image en modulo n est également juste.
Si une opération est juste,
son image en modulo n est également juste.
 En modulo 9; c'est la preuve
par neuf.
En modulo 9; c'est la preuve
par neuf.
|
*
|
>>>
>>>
|
|
mo3
|
Modulo
|
 En modulo n, si a
En modulo n, si a 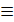 a' et b a' et b 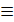 b', alors a+b b', alors a+b 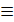 a'+b' et ab a'+b' et ab 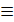 a'b' a'b'
|
**
|
>>>
|
|
mo4
|
Modulo
|
 Entiers m1, m2
… mk étrangers deux à deux; des nombres
ai chacun compris entre 0 et mi ; il existe un nombre
n, unique modulo m1 m2 … mk
tel que: n
Entiers m1, m2
… mk étrangers deux à deux; des nombres
ai chacun compris entre 0 et mi ; il existe un nombre
n, unique modulo m1 m2 … mk
tel que: n 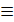 ai mod m pour i de 1 à k. ai mod m pour i de 1 à k.
Théorème
chinois
|
***S
|
|
|
nb1
|
Nombre
|
 Tout nombre est décomposable
de façon unique en produit de nombres premiers (à l'ordre près).
Tout nombre est décomposable
de façon unique en produit de nombres premiers (à l'ordre près).
Théorème fondamental de l'arithmétique
|
**S
|
>>>
|
|
nb2
|
Nombre
|
 Tout nombre est la somme de
trois nombres triangulaires.
Tout nombre est la somme de
trois nombres triangulaires.
 Tout nombre est la somme de
quatre carrés.
Tout nombre est la somme de
quatre carrés.
Théorème de Lagrange
 Tout nombre est la somme de
neuf cubes.
Tout nombre est la somme de
neuf cubes.
 Tout nombre est la somme de r
puissances k.
Tout nombre est la somme de r
puissances k.
Théorème de Waring
|
**S
***
|
>>>
>>>
|
|
nu1
|
Numération
|
 Tout nombre entier naturel N s'écrit de manière unique
comme somme de puissances de 10 pour les nombres décimaux et puissances de B
pour toute base B.
Tout nombre entier naturel N s'écrit de manière unique
comme somme de puissances de 10 pour les nombres décimaux et puissances de B
pour toute base B.
|
***
|
>>>
|
|
pr1
|
Premier
|
 Tout nombre premier est de la
forme 4n
Tout nombre premier est de la
forme 4n 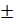 1 1
 Tout nombre premier est de la
forme 6n
Tout nombre premier est de la
forme 6n 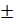 1 1
|
**
|
>>>
>>>
|
|
pr2
|
Premier
|
 Tout nombre pair est la somme
de deux nombres premiers.
Tout nombre pair est la somme
de deux nombres premiers.
 Tout nombre impair est la
somme de trois nombres premiers.
Tout nombre impair est la
somme de trois nombres premiers.
Conjecture de Goldbach
|
***S
|
>>>
|
|
pr3
|
Premier
|
 Les nombres premiers sont en nombre infinis
Les nombres premiers sont en nombre infinis
|
*
|
>>>
|
|
pr4
|
Premier
|
 Le nième nombre premier est inférieur
à 2n
Le nième nombre premier est inférieur
à 2n
|
***
|
>>>
|
|
pr5
|
Premier
|
 La quantité de nombres premiers au
plus égaux à n est aussi près que l'on veut de n / log(n), il suffit de
choisir n assez grand.
La quantité de nombres premiers au
plus égaux à n est aussi près que l'on veut de n / log(n), il suffit de
choisir n assez grand.
|
***S
|
>>>
|
|
pr6
|
Premier
|
 Il est possible de trouver une suite de nombres
composés successifs aussi longue que souhaitée.
Il est possible de trouver une suite de nombres
composés successifs aussi longue que souhaitée.
|
**
|
>>>
|
|
so1
|
Somme
|
 La somme des n premiers
nombres entiers vaut: n(n+1)/2
La somme des n premiers
nombres entiers vaut: n(n+1)/2
|
*
|
>>>
|
|
so2
|
Somme
|
 Un nombre en 4k + 3 n'est pas
décomposable en somme de deux carrés.
Un nombre en 4k + 3 n'est pas
décomposable en somme de deux carrés.
|
***
|
>>>
|
|
su1
|
Suite
|
 Deux nombres de Fibonacci consécutifs sont étrangers:
PGCD (Fn , Fn+1) = 1.
Deux nombres de Fibonacci consécutifs sont étrangers:
PGCD (Fn , Fn+1) = 1.
|
**
|
>>>
|
|
su2
|
Suite
|
 La somme d'une progression arithmétique de n termes, de
raison r et de premier terme a est égale à
La somme d'une progression arithmétique de n termes, de
raison r et de premier terme a est égale à
|
**
|
>>>
|
|
su3
|
Suite
|
 Aucune suite de quatre carrés n'est en progression arithmétique.
Aucune suite de quatre carrés n'est en progression arithmétique.
|
**
|
>>>
|
|
tr1
|
Triplets
|
 Il existe une infinité de
triplets a² + b² = c², comme 3² + 4² = 5².
Il existe une infinité de
triplets a² + b² = c², comme 3² + 4² = 5².
 Ils sont de la forme 2pq, q²
- p², q² + p².
Ils sont de la forme 2pq, q²
- p², q² + p².
Triplets de Pythagore
|
*S
|
>>>
|
|
tr2
|
Triplets
|
 Il n'existe aucun triplet de
la forme Xn + Yn
= Zn
Il n'existe aucun triplet de
la forme Xn + Yn
= Zn
Théorème de Fermat-Wiles
|
**S
|
>>>
|
|
tr3
|
Triplets
|
 Si n > 2 est premier, ainsi que 2n + 1,
alors xn + yn
= zn implique que l'un des nombres (x, y
ou z) est divisible par n.
Si n > 2 est premier, ainsi que 2n + 1,
alors xn + yn
= zn implique que l'un des nombres (x, y
ou z) est divisible par n.
Théorème
de Sophie Germain
|
***
|
>>>
|
|
ty1
|
Type
|
 La racine de tout nombre entier, hors puissance
entière, est irrationnelle. Ses décimales se poursuivent sans fin sans
répétition.
La racine de tout nombre entier, hors puissance
entière, est irrationnelle. Ses décimales se poursuivent sans fin sans
répétition.
|
**
|
>>>
|
|
fr1
|
Fraction
|
 Toute fraction unitaire est la somme de trois
fractions: 1/n = 1/2n + 1/3n + 1/6n.
Toute fraction unitaire est la somme de trois
fractions: 1/n = 1/2n + 1/3n + 1/6n.
|
*
|
>>>
|
|
di1
|
Différence
|
 Tout nombre impair est différence de deux carrés de
nombres consécutifs
Tout nombre impair est différence de deux carrés de
nombres consécutifs
 Tout nombre pair est différence de deux carrés de deux
nombres pairs consécutifs
Tout nombre pair est différence de deux carrés de deux
nombres pairs consécutifs
|
*
|
>>>
|
|
pu1
|
Cubes
|
 La somme des cubes des nombres successifs est le carré
de la somme de ces nombres
La somme des cubes des nombres successifs est le carré
de la somme de ces nombres
 Cette somme des cubes est divisible par la somme des
nombres
Cette somme des cubes est divisible par la somme des
nombres
|
**
|
>>>
|
|
pu2
|
Carrés
|
 Deux nombres consécutifs: la différence de leur carré
est égale à leur somme
Deux nombres consécutifs: la différence de leur carré
est égale à leur somme
|
**
|
|
|
pu2
|
Carrés
|
 Carré d'un nombre impair: unité impaire et dizaine
paire
Carré d'un nombre impair: unité impaire et dizaine
paire
|
**
|
>>>
|
|
pu3
|
Cubes
|
 Cube d'un nombre impair: unité impaire et dizaine conserve
la parité du nombre.
Cube d'un nombre impair: unité impaire et dizaine conserve
la parité du nombre.
|
**
|
>>>
|
![]()